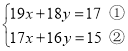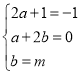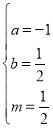Question

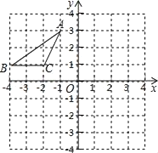
【题目】如图，平行四边形ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于 的一元二次方程 的两个根，且OA＞OB

（1）求cos∠ABC的值。
（2）若E为x轴上的点，且 ，求出点E的坐标，并判断△AOE与△DAO是否相似？请说明理由

Answer 1

【答案】
（1）解：解一元二次方程 得 ， ∵OA＞OB ∴OA＝4，OB＝3，

在 ，

∴ ，

∴cos∠ABC=

（2）解：设E（x，0），由题意得 解得 ∴E（ ，0）或（ ，0）， ∵四边形ABCD是平行四边形，

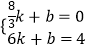∴点D的坐标是（6，4） 设经过D、E两点的直线的解析式为 若图象过点（ ，0），（6，4） 则 ，解得 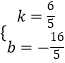此时函数解析式为

若图象过点（ ，0），（6，4） 则 ，解得 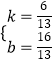此时函数解析式为

在△AOE与△DAO中， ，

∴

又∵∠AOE=∠OAD=90°

∴△AOE∽△DAO。

【解析】（1）可先解一元二次方程求出OA，OB的长度，再利用勾股定理求出AB的长度，利用余弦定义计算得出结果；
（2）先根据三角形的面积求出OE，再转化为坐标，有两种情况，，并根据平行四边形的对边相等的性质求出点D的坐标，然后利用待定系数法求解直线的解析式；分别求出两三角形夹直角的两对应边的比，如果相等，则两三角形相似，否则不相似；