题目内容
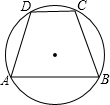 如图,四边形ABCD是⊙O的内接四边形,AB∥CD,AB=4,CD=2,并且
如图,四边形ABCD是⊙O的内接四边形,AB∥CD,AB=4,CD=2,并且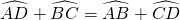 ,则四边形ABCD的面积为
,则四边形ABCD的面积为
- A.6
- B.9
- C.12
- D.18
B
分析:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,由AB∥CD,得到OF⊥AB,根据垂径定理得到DE=EC=1,DM弧=MC弧,AF=BF=2,AN弧=BN弧,而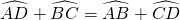 ,则AD弧为半圆MN的一半,得到∠DOA=90°,易证Rt△ODE≌Rt△OAF,
,则AD弧为半圆MN的一半,得到∠DOA=90°,易证Rt△ODE≌Rt△OAF,
则OE=AF=2,OF=DE=1,即EF=3,然后利用梯形的面积公式计算即可.
解答: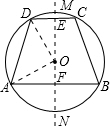 解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,
解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,
∴DE=EC=1,DM弧=MC弧,
∵AB∥CD,
∴OF⊥AB,AD弧=BC弧,
∴AF=BF=2,AN弧=BN弧,
而且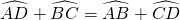 ,
,
∴AD弧=DM弧+AN弧,
∴AD弧为半圆MN的一半,
∴∠DOA=90°,
∴Rt△ODE≌Rt△OAF,
∴OE=AF=2,OF=DE=1,即EF=3,
∴梯形ABCD的面积= •(2+4)•3=9.
•(2+4)•3=9.
故选B.
点评:本题考查了圆的内接四边形的性质:对角互补;也考查了垂径定理和梯形的面积公式以及三角形全等的判定与性质.
分析:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,由AB∥CD,得到OF⊥AB,根据垂径定理得到DE=EC=1,DM弧=MC弧,AF=BF=2,AN弧=BN弧,而
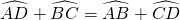 ,则AD弧为半圆MN的一半,得到∠DOA=90°,易证Rt△ODE≌Rt△OAF,
,则AD弧为半圆MN的一半,得到∠DOA=90°,易证Rt△ODE≌Rt△OAF,则OE=AF=2,OF=DE=1,即EF=3,然后利用梯形的面积公式计算即可.
解答:
 解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,
解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,∴DE=EC=1,DM弧=MC弧,
∵AB∥CD,
∴OF⊥AB,AD弧=BC弧,
∴AF=BF=2,AN弧=BN弧,
而且
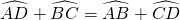 ,
,∴AD弧=DM弧+AN弧,
∴AD弧为半圆MN的一半,
∴∠DOA=90°,
∴Rt△ODE≌Rt△OAF,
∴OE=AF=2,OF=DE=1,即EF=3,
∴梯形ABCD的面积=
 •(2+4)•3=9.
•(2+4)•3=9.故选B.
点评:本题考查了圆的内接四边形的性质:对角互补;也考查了垂径定理和梯形的面积公式以及三角形全等的判定与性质.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.