题目内容
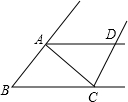
如图,△ABC∽△DEC,CA=CB,且点E在AB的延长线上.求证:(1)AE=BD;
(2)△BOE∽△COD.

【答案】分析:(1)利用相似三角形的性质:对应边的比值相等可证明CE=CD,再根据全等三角形的判定方法可证明△ACE≌△CBD,进而证明AE=BD;
(2)利用有两对角相等的两三角形相似即可证明:△BOE∽△COD.
解答:证明(1)∵△ABC∽△DEC,
∴ ,∠ACB=∠DCE,
,∠ACB=∠DCE,
∵CA=CB,
∴CE=CD,
∵∠ACE=∠ACB+∠BCE,∠BCD=∠DCE+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△CBD中,
∵ ,
,
∴△ACE≌△CBD.
∴AE=BD;
(2)∵∠DCE=∠DBE,∠DOC=∠BOE,
∴△BOE∽△COD.
点评:本题考查了相似三角形的性质和判定以及全等三角形的性质和判定,证明时注意图形中隐藏条件的挖掘如:公共角和对顶角.
(2)利用有两对角相等的两三角形相似即可证明:△BOE∽△COD.
解答:证明(1)∵△ABC∽△DEC,
∴
 ,∠ACB=∠DCE,
,∠ACB=∠DCE,∵CA=CB,
∴CE=CD,
∵∠ACE=∠ACB+∠BCE,∠BCD=∠DCE+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△CBD中,
∵
 ,
,∴△ACE≌△CBD.
∴AE=BD;
(2)∵∠DCE=∠DBE,∠DOC=∠BOE,
∴△BOE∽△COD.
点评:本题考查了相似三角形的性质和判定以及全等三角形的性质和判定,证明时注意图形中隐藏条件的挖掘如:公共角和对顶角.

练习册系列答案
相关题目
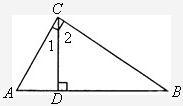
 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
 ,且CB=CE.
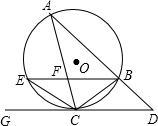
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.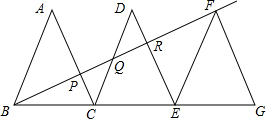 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且