题目内容
一个三位数,百位数是a,十位数是b,个位数是c,且a>b,把百位数与个位数的位置交换得到一个新的三位数.试说明:原三位数与新三位数的差一定是99的倍数.
考点:整式的加减
专题:
分析:由原来三位数的个位数字为a,十位数字为b,百位数字为c,得出三位数为100a+10b+c,然后根据题意列出新数为100c+10b+a,求得与原数的差整理即可得出答案.
解答:解:由题意得
(100a+10b+c)-(100c+10b+a)
=100a+10b+c-100c-10b-a
=99a-99c
=99(a-c).
所以原三位数与新三位数的差一定是99的倍数.
(100a+10b+c)-(100c+10b+a)
=100a+10b+c-100c-10b-a
=99a-99c
=99(a-c).
所以原三位数与新三位数的差一定是99的倍数.
点评:本题考查了整式的加减,掌握数的表示方法是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知:△ABC内接于圆O,点D在OC的延长线上,若∠B=∠D=30°
如图,已知:△ABC内接于圆O,点D在OC的延长线上,若∠B=∠D=30°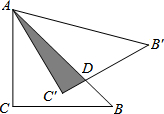 如图,△ABC为等腰直角三角形,AC=CB,∠ACB=90°,将△ABC绕点A逆时针旋转后得到△AB′C′,若AC=6cm,△AB′C′与△ABC重叠部分面积为6
如图,△ABC为等腰直角三角形,AC=CB,∠ACB=90°,将△ABC绕点A逆时针旋转后得到△AB′C′,若AC=6cm,△AB′C′与△ABC重叠部分面积为6