题目内容
 如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点,
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点,
则PC+PD的最小值为________.
7
分析:要求PC+PD的和的最小值,PC,PD不能直接求,可考虑通过作辅助线转化PC,PD的值,从而找出其最小值求解.
解答: 解:延长CB到E,使EB=CB=8,连接DE交AB于P.则DE就是PC+PD的和的最小值.
解:延长CB到E,使EB=CB=8,连接DE交AB于P.则DE就是PC+PD的和的最小值.
∵AD∥BE,
∴∠A=∠PBE,∠ADP=∠E,
∴△ADP∽△BEP,
∴AP:BP=AD:BE=6:8=3:4,
∴PB= AP,
AP,
∵AP+BP=AB=7,
∴AP=3,BP=4,
∴PD= =
=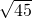 =3
=3 ,PE=
,PE= =4
=4 ,
,
∴DE=PD+PE=7 ,
,
∴PC+PD的最小值是7 ,
,
故答案为:7 .
.
点评:此题考查了轴对称的性质、勾股定理的运用及相似三角形的判定和性质,解题时要注意找到对称点,并根据“两点之间线段最短”确定P点的位置.

分析:要求PC+PD的和的最小值,PC,PD不能直接求,可考虑通过作辅助线转化PC,PD的值,从而找出其最小值求解.
解答:
 解:延长CB到E,使EB=CB=8,连接DE交AB于P.则DE就是PC+PD的和的最小值.
解:延长CB到E,使EB=CB=8,连接DE交AB于P.则DE就是PC+PD的和的最小值.∵AD∥BE,
∴∠A=∠PBE,∠ADP=∠E,
∴△ADP∽△BEP,
∴AP:BP=AD:BE=6:8=3:4,
∴PB=
 AP,
AP,∵AP+BP=AB=7,
∴AP=3,BP=4,
∴PD=
 =
=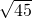 =3
=3 ,PE=
,PE= =4
=4 ,
,∴DE=PD+PE=7
 ,
,∴PC+PD的最小值是7
 ,
,故答案为:7
 .
.点评:此题考查了轴对称的性质、勾股定理的运用及相似三角形的判定和性质,解题时要注意找到对称点,并根据“两点之间线段最短”确定P点的位置.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
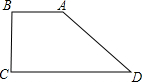 如图所示,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AD=20,BC=10,则∠A和∠D分别是( )
如图所示,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AD=20,BC=10,则∠A和∠D分别是( )| A、30°,150° | B、45°,135° | C、120°,60° | D、150°,30° |
 27、如图所示,在直角梯形ABCD中,AD∥BC,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边向B以3cm/s的速度运动.P,Q分别从A,C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t(s),t分别为何值时,四边形PQCD是平行四边形?等腰梯形?
27、如图所示,在直角梯形ABCD中,AD∥BC,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边向B以3cm/s的速度运动.P,Q分别从A,C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t(s),t分别为何值时,四边形PQCD是平行四边形?等腰梯形?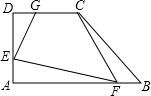 如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围. 如图所示,在直角梯形ABCD中,AB=2,P是边AB的中点,∠PDC=90°,问梯形ABCD面积的最小值是多少?
如图所示,在直角梯形ABCD中,AB=2,P是边AB的中点,∠PDC=90°,问梯形ABCD面积的最小值是多少? (2013•山西模拟)如图所示,在直角梯形ABCD中,AB∥CD,点E为AB的中点,点F为BC的中点,AB=4,EF=2,∠B=60°,则AD的长为
(2013•山西模拟)如图所示,在直角梯形ABCD中,AB∥CD,点E为AB的中点,点F为BC的中点,AB=4,EF=2,∠B=60°,则AD的长为