Question

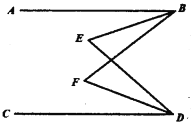
【题目】如图，在平行四边形中，的平分线交于点，的平分线交于点．

求证：四边形是平行四边形．

Answer 1

【答案】详见解析

【解析】

根据平行四边形性质得出AB=CD，∠A=∠C．求出∠ABD=∠CDB．推出∠ABE=∠CDF，根据ASA推出△ABE≌△CDF即可证得DE=BF；再又DE∥BF可得．

证明：在□ABCD中，AB=CD，∠A=∠C,AD=BC．

∵AB∥CD，

∴∠ABD=∠CDB．

∵BE平分∠ABD，DF平分∠CDB，

∴∠ABE=∠ABD，∠CDF=∠CDB．

∴∠ABE=∠CDF．

∵在△ABE和△CDF中，

∴△ABE≌△CDF（ASA）．

∴AE=CF

∴AD-AE=BC-CF,即DE=BF

又AD∥BC

∴四边形DEBF是平行四边形