题目内容
如图,已知C为线段AB上一点,△ACM和△BCN都是等边三角形.

(1)求证:AN=BM;
(2)若把原题中“△ACM和△BCN都是等边三角形”换成“四边形ACMF和四边形CBEN都是正方形”(如图所示),那么AN与BM的关系如何?请说明理由.

答案:
解析:
解析:
|
解:(1)证明:因为△ACM、△BCN都是等边三角形,所以∠ACM=∠BCN=60°,AC=CM,CN=CB. 所以∠ACM+∠MCN=∠BCN+∠MCN, 即∠ACN=∠MCB. 在△ACN和△MCB中, 因为AC=MC,∠ACN=∠MCB,CN=CB, 所以△ACN≌△MCB.所以AN=MB. (2)AN=BM. 理由:因为四边形ACMF和四边形CBEN都是正方形, 所以AC=MC,CN=CB,∠ACN=∠MCB=90°. 在△ACN和△MCB中, 因为AC=MC,∠ACN=∠MCB,CN=CB, 所以△ACN≌△MCB.所以AN=BM. |

练习册系列答案
相关题目
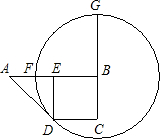 的⊙B与AB边相交于F点,延长CB交⊙B于G点.
的⊙B与AB边相交于F点,延长CB交⊙B于G点. 如图,已知C为线段AB的中点,D在线段CB上.若DA=6,DB=4,则CD=
如图,已知C为线段AB的中点,D在线段CB上.若DA=6,DB=4,则CD= 如图,已知C为线段AB的中点,D为线段AC的中点.如果线段DC=3cm,那么AB=
如图,已知C为线段AB的中点,D为线段AC的中点.如果线段DC=3cm,那么AB=