Question

【题目】如图，一次函数y＝－x＋b与反比例函数y＝ (x＞0)的图象交于A，B两点，与x轴、y轴分别交于C，D两点，连接OA，OB，过A作AE⊥x轴于点E，交OB于点F，设点A的横坐标为m.

(1)b＝________(用含m的代数式表示)；

(2)若S△OAF＋S四边形EFBC＝4，则m的值是________．

Answer 1

【答案】 m+

【解析】（1）∵点A在函数的图象上，且A的横坐标为，

∴点A的纵坐标为，

又∵点A在一次函数的图象上，

∴，解得；

（2）如下图，过点A作AM⊥OD于点M，过点B作BN⊥OC于点N，

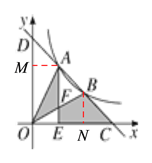
∵函数与的图象都关于直线对称，

∴AM=BN=OE，△DOA≌△COB，

设△OAF的面积为，∵S△OAE =2，S△OAF＋S四边形EFBC＝4，

∴S△OEF=S△OAE- = ，S四边形EFBC = ，

∴S△DOA=S△COB=S△OEF+ S四边形EFBC =，

∴S△ADM= S△DOA - S△OAM =，

∴S△ADM =2 S△OEF，

又∵OE=MA，

∴EF=AM=BN，

由EF∥BN可知△OEF∽△OBN，∴

∴点E是ON的中点，

∴ON=2OE=2AM=，

∴点B的坐标为，

把B的坐标代入得： ，解得，

又∵，

∴.