题目内容
 如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=
如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE= :4,其中正确结论的个数是
:4,其中正确结论的个数是
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:①根据已知得出∠CAF=30°,∠GAF=60°,进而得出∠AFB的度数;②利用ASA证明△ADG≌△ACF得出答案;
③利用△AGO≌△AFO,得出AO=CO=AC,进而得出BO=CO=AO,即O为BC的中点;④利用假设DG=x,∠DAG=30°,得出AG= x,GE=3x,进而得出答案.
x,GE=3x,进而得出答案.
解答:∵两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.
∴∠CAF=30°,
∴∠GAF=60°,
∴∠AFB=90°,
①AF丄BC正确;
∵AD=AC,∠DAG=∠CAF,
∠D=∠C=60°,
即可得②△ADG≌△ACF正确;
∵△ADG≌△ACF,
∴AG=AF,
∵AO=AO,
∠AGO=∠AFO=90°,
∴△AGO≌△AFO,
∴∠OAF=30°,
∴∠OAC=60°,
∴AO=CO=AC,
BO=CO=AO,
即可得③正确;
假设DG=x,
∵∠DAG=30°,
∴AG= x,
x,
∴GE=3x,
故可得AG:DE= :4,即④正确;
:4,即④正确;
综上可得①②③④均正确,共4个.
故选D.
点评:此题主要考查了全等三角形的判定以及30°所对直角边的性质和直角三角形的性质,根据三角形全等得出个边对应情况是解决问题的关键.
分析:①根据已知得出∠CAF=30°,∠GAF=60°,进而得出∠AFB的度数;②利用ASA证明△ADG≌△ACF得出答案;
③利用△AGO≌△AFO,得出AO=CO=AC,进而得出BO=CO=AO,即O为BC的中点;④利用假设DG=x,∠DAG=30°,得出AG=
 x,GE=3x,进而得出答案.
x,GE=3x,进而得出答案.解答:∵两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.
∴∠CAF=30°,
∴∠GAF=60°,
∴∠AFB=90°,
①AF丄BC正确;
∵AD=AC,∠DAG=∠CAF,
∠D=∠C=60°,
即可得②△ADG≌△ACF正确;
∵△ADG≌△ACF,
∴AG=AF,
∵AO=AO,
∠AGO=∠AFO=90°,
∴△AGO≌△AFO,
∴∠OAF=30°,
∴∠OAC=60°,
∴AO=CO=AC,
BO=CO=AO,
即可得③正确;
假设DG=x,
∵∠DAG=30°,
∴AG=
 x,
x,∴GE=3x,
故可得AG:DE=
 :4,即④正确;
:4,即④正确;综上可得①②③④均正确,共4个.
故选D.
点评:此题主要考查了全等三角形的判定以及30°所对直角边的性质和直角三角形的性质,根据三角形全等得出个边对应情况是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
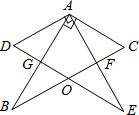 如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF丄BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=
如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF丄BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE= 如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=
如图所示,两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.有以下四个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG:DE=
 :4,其中正确结论的序是①②③④ .(错填得0分,少填酌情给分).
:4,其中正确结论的序是①②③④ .(错填得0分,少填酌情给分).
 ,其中正确结论的序号是 .
,其中正确结论的序号是 .