题目内容
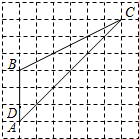
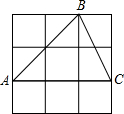 如图,在正方形网格中,sin∠ABC=________.
如图,在正方形网格中,sin∠ABC=________.

分析:连接CD,作CE⊥AB于E,根据勾股定理可以求得BC、BD、CD的长,根据三线合一定理求得BE的长,再根据勾股定理求得EC的长,根据正弦的定义即可求解.
解答:
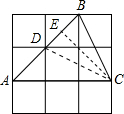 解:连接CD,作CE⊥AB于E.
解:连接CD,作CE⊥AB于E.设正方形网格的每个小正方形的边长是1,则根据勾股定理可得:BD=
 ,CD=BC=
,CD=BC= ,
,∵CD=BC,CE⊥BD,
∴BE=
 BD=
BD= ,
,则在直角△BCE中,EC=
 =
= =
= ,
,则sin∠ABC=
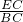 =
= =
= .
.故答案是:
 .
.点评:本题考查了正弦的定义以及三线合一定理,正确求得EC的长度是关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
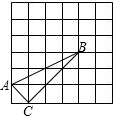 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
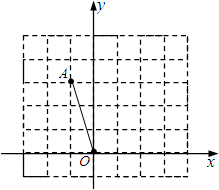 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).