题目内容
人民币1993年版的一角硬币正面图案中有一个正九边形,如果设这个正九边形的半径为R,那么它的周长是
- A.9Rsin20°
- B.9Rsin40°
- C.18Rsin20°
- D.18Rsin40°
C
分析:连接OA、OB,过O作OM⊥AB于M,根据正九边形得出AB=BC=CD=DE=EF=GF=GH=HI=AI,∠AOB=40°,在△AOM中求出AM=OAsin20°=Rsin20°,根据三线合一定理得出AB=2AM=2Rsin20°,即可求出正九边形的周长.
解答: 解:连接OA、OB,过O作OM⊥AB于M,
解:连接OA、OB,过O作OM⊥AB于M,
则OA=OB=R,
∵九边形ABCDEFGHI是正九边形,
∴AB=BC=CD=DE=EF=GF=GH=HI=AI,∠AOB= =40°,
=40°,
在△AOM中,sin∠AOM=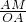 ,
,
AM=OAsin20°=Rsin20°,
∵OA=OB,OM⊥AB,
∴AB=2AM=2Rsin20°,
即正九边形的周长是9×2Rsin20°=18Rsin20°,
故选C.
点评:本题考查了正多边形的性质,等腰三角形性质,锐角三角函数的定义等知识点,关键是正确作辅助线和求出AM的长.
分析:连接OA、OB,过O作OM⊥AB于M,根据正九边形得出AB=BC=CD=DE=EF=GF=GH=HI=AI,∠AOB=40°,在△AOM中求出AM=OAsin20°=Rsin20°,根据三线合一定理得出AB=2AM=2Rsin20°,即可求出正九边形的周长.
解答:
 解:连接OA、OB,过O作OM⊥AB于M,
解:连接OA、OB,过O作OM⊥AB于M,则OA=OB=R,
∵九边形ABCDEFGHI是正九边形,
∴AB=BC=CD=DE=EF=GF=GH=HI=AI,∠AOB=
 =40°,
=40°,在△AOM中,sin∠AOM=
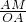 ,
,AM=OAsin20°=Rsin20°,
∵OA=OB,OM⊥AB,
∴AB=2AM=2Rsin20°,
即正九边形的周长是9×2Rsin20°=18Rsin20°,
故选C.
点评:本题考查了正多边形的性质,等腰三角形性质,锐角三角函数的定义等知识点,关键是正确作辅助线和求出AM的长.

练习册系列答案
相关题目
 1993年版人民币的一角硬币正面图案中有一个正九边形,如果这个正九边形的半径是R,那么它的边长是( )
1993年版人民币的一角硬币正面图案中有一个正九边形,如果这个正九边形的半径是R,那么它的边长是( )| A、Rsin20° | B、Rsin40° | C、2Rsin20° | D、2Rsin40° |