题目内容
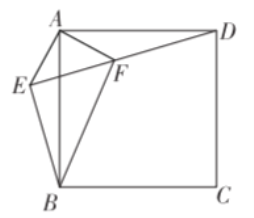
【题目】纸片![]() 中,
中,![]() ,将它折叠使
,将它折叠使![]() 与
与![]() 重合,折痕
重合,折痕![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长为________.
的长为________.
【答案】6或10
【解析】
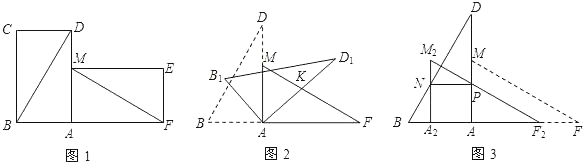
如下图,过点A作BC垂线交BC于点D,△ABD是含有30°的直角三角形,已知AB,则可得到AD的长;根据折叠的性质,可得△BCM是正三角形,设MB=x,则可得到DC=x-8;在Rt△ADC中,利用勾股定理可得到一个关于x的方程,解得结果即为BM长,进而得出MA长
情况一:如下图,△ABC是锐角三角形,过点A作BC垂线交BC于点D
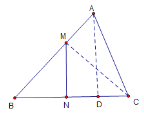
∵∠B=60°,AB=16,AD⊥BC
∴在Rt△ABD中,BD=8,AD=![]()
∵△MCN是△MBN折叠得到,∴∠MCB=∠B=60°
∴△MBC为正三角形,∴MB=BC
设MB=x,则BC=x,DC=x-8
∵AC=14
∴在Rt△ADC中,![]() ,即
,即![]()
解得:x=6(舍)或x=10,∴AM=6
情况二:如下图,当△ABC是钝角三角形,过点A作BC垂线交BC于点D
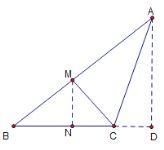
同理,BD=8,AD=![]() ,△MBC为正三角形
,△MBC为正三角形
设MB=x,则BC=x,CD=8-x
∵AC=14
∴在Rt△ADC中,![]() ,即
,即![]()
解得:x=6或x=10(舍),∴AM=10
综上得:AM=10或AM=6
故答案为:6或10

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目