题目内容
 如图,正方形网格中,每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转180°.试解决下列问题:
如图,正方形网格中,每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转180°.试解决下列问题:(1)画出四边形ABCD旋转后的图形;
(2)设点C旋转后的对应点为C′,则tan∠AC′B=
| 2 |
| 3 |
| 2 |
| 3 |
(3)求点C旋转过程中所经过的路径长.
分析:(1)连接BO、CO并延长相同单位找到对应点,顺次连接即可.
(2)先利用网格得出△EBC′为直角三角形,再根据正切函数定义计算.
(3)点C旋转过程所经过的路径是一段弧线,根据弧长公式即可计算.
(2)先利用网格得出△EBC′为直角三角形,再根据正切函数定义计算.
(3)点C旋转过程所经过的路径是一段弧线,根据弧长公式即可计算.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
连接BC′,在Rt△EBC′中,
tan∠AC′B=
=
,
故答案为:
;

(3)如图所示:点C旋转过程中所经过的路径长,即为以O为圆心,CO长为半径的弧,
∵CO=
=
,
∴点C旋转过程中所经过的路径长为:
=
π.
 解:(1)如图所示:
解:(1)如图所示:(2)如图所示:
连接BC′,在Rt△EBC′中,
tan∠AC′B=
| BE |
| EC′ |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |

(3)如图所示:点C旋转过程中所经过的路径长,即为以O为圆心,CO长为半径的弧,
∵CO=
| 22+12 |
| 5 |
∴点C旋转过程中所经过的路径长为:
180π×
| ||
| 180 |
| 5 |
点评:本题考查了旋转变换作图和弧长公式的计算方法及解直角三角形,根据已知在Rt△EBC′中求出tan∠AC′B的值是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
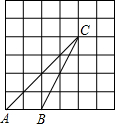 在如图的正方形网格中有一个格点三角形ABC.请在图中画一个与△ABC相似且相似比不等于1的格点三角形,并写出它们的相似比.
在如图的正方形网格中有一个格点三角形ABC.请在图中画一个与△ABC相似且相似比不等于1的格点三角形,并写出它们的相似比.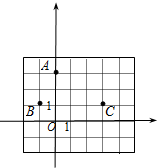 22、如图,正方形网格中,A、B、C均在格点上,在所给直角坐标系中解答下列问题:
22、如图,正方形网格中,A、B、C均在格点上,在所给直角坐标系中解答下列问题: 在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.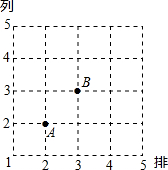 如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.
如图,正方形网格中的交点,我们称之为格点,点A用有序数对(2,2)表示,其中第一个数表示排数,第2个数表示列数,在图中有一个格点C,使S△ABC=1,写出符合条件的点C的有序数对.