题目内容
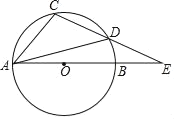
【题目】如图,AB是⊙O的直径,△ACD内接于⊙O,延长AB,CD相交于点E,若∠CAD=35°,∠CDA=40°,则∠E的度数是( )
A.20°B.25°C.30°D.35°
【答案】B
【解析】
连接BD,由AB是⊙O的直径可得∠ADB=90°,根据三角形内角和定理可求出∠ACD的度数,进一步根据圆内接四边形的性质可求得∠ABD的度数,从而可得∠BAD的度数,然后根据三角形的外角性质定理可得结果.
解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
由三角形内角和定理得,∠ACD=180°﹣∠CAD﹣∠CDA=105°,
∴∠ABD=180°﹣∠ACD=75°,
∴∠BAD=90°﹣∠ABD=15°,
∴∠E=∠CDA﹣∠DAB=25°,
故选:B.


练习册系列答案
相关题目