Question

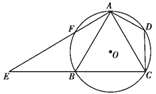
【题目】如图,已知四边形ABCD内接于☉O,A是的中点,AE⊥AC于A,与☉O及CB的延长线交于点F、E,且=.

(1)求证:△ADC∽△EBA;

(2)如果AB=8,CD=5,求tan∠CAD的值.

Answer 1

【答案】(1)见解析;(2)

【解析】分析：（1）欲证△ADC∽△EBA，只要证明两个角对应相等就可以．可以转化为证明且=就可以；
（2）A是的中点，的中点，则AC=AB=8，根据△CAD∽△ABE得到∠CAD=∠AEC，求得AE，根据正切三角函数的定义就可以求出结论．

详解：(1)证明:∵四边形ABCD内接于☉O,

∴∠CDA=∠ABE.

∵=,

∴∠DCA=∠BAE,

∴△ADC∽△EBA.

(2)∵A是的中点,

∴=,

∴AB=AC=8.

∵△ADC∽△EBA,

∴∠CAD=∠AEC,=,即=,

∴AE=,

∴tan∠CAD=tan∠AEC===.