题目内容
已知:如图,正方形ABCD中,点E是CD上一点,点F是CB的延长线上一点,且EA⊥AF。求证:DE=BF.
证明:∵四边形ABCD是正方形
∴AB=AD,∠BAD=∠ADE=∠ABF=90°
又∵EA⊥AF
∴∠BAF+∠BAE=∠BAE+∠DAE=90
∴∠BAF=∠DAE
又∵在Rt△ABF和Rt△ADE中

 ∴Rt△ABF≌Rt△ADE(AAS) ∴DE=BF
∴Rt△ABF≌Rt△ADE(AAS) ∴DE=BF

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.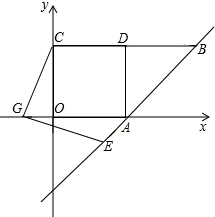
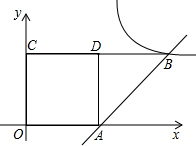
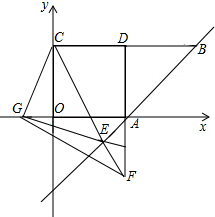



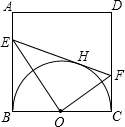 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.