Question

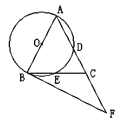
【题目】如图，以点O为圆心的三个同心圆把以OA1为半径的大圆的面积四等分，若OA1=R,则OA4:OA3:OA2:OA1=______________,若有（）个同心圆把这个大圆等分，则最小的圆的半径是=_______．

Answer 1

【答案】

【解析】

根据每个圆与大圆的面积关系，即可求出每个圆的半径长，即可得到结论.

∵πOA42＝πOA12，
∴O A42＝OA12，
∴O A4=OA1；
∵πOA32＝πOA12，
∴O A32＝OA12，
∴O A3=OA1；
∵πOA22＝πOA12，
∴O A22＝OA12，
∴O A2=OA1；

∵OA1=R
因此这三个圆的半径为：O A2=R，O A3=R，O A4=R．

∴OA4:OA3:OA2:OA1=

由此可得，有（）个同心圆把这个大圆等分，则最小的圆的半径是=

故答案为：（1）；（2）．