题目内容
 已知正方形ABCD,点E在边AB上,以CE为边作正方形CEFG,如图所示,连接DG.求证:△BCE≌△DCG.甲、乙两位同学的证明过程如下,则下列说法正确的是( )
已知正方形ABCD,点E在边AB上,以CE为边作正方形CEFG,如图所示,连接DG.求证:△BCE≌△DCG.甲、乙两位同学的证明过程如下,则下列说法正确的是( )甲:∵四边形ABCD、四边形CEFG都是正方形
∴CB=CD CE=CG∠BCD=∠ECG=90°
∴∠BCD-∠ECD=∠ECG-∠ECD
∴∠BCE=∠GCD
∴△BCE≌△DCG(SAS)
乙:∵四边形AB,CD、四边形CEFG都是正方形
∴CB=CD CE=CG
且∠B=∠CDG=90°
∴△BCE≌△DCG(HL)
分析:根据正方形性质得出BC=CD,CE=CG,∠BCD=∠ECG=90°,都减去∠ECD,即可求出∠BCE=∠DCG,根据SAS即可推出两三角形全等;但是根据已知不能推出∠CDG=90°,即可判断乙同学证明过程不对.
解答:解:甲同学的证明过程正确;而乙同学的证明过程错误;
因为从已知不能确定A、D、G三点共线,
即不能推出∠GDC=90°,
故选A.
因为从已知不能确定A、D、G三点共线,
即不能推出∠GDC=90°,
故选A.
点评:本题考查了全等三角形的判定和正方形性质,主要考查学生的推理能力和辨析能力.

练习册系列答案
相关题目
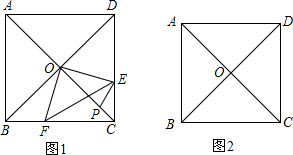
 直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2.
直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2. 已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.
已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.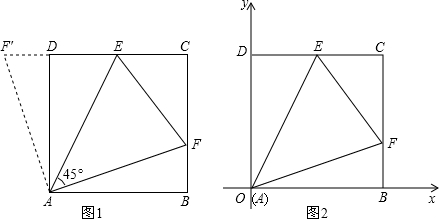
 如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.
如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.