题目内容
如图,在△ 中,
中, 平分∠
平分∠ ,
, ,
, 交
交 的延长线于点
的延长线于点 ,点
,点 在
在 上,且
上,且 ∥
∥ 。求证:点
。求证:点 是
是 的中点.
的中点.

【答案】
见解析
【解析】证明:∵ 平分
平分 ,
,
∴
∵ ∥
∥
∴
∴
又 ∵
∴ ,
,
∴
∴
∴
∴ 为
为 中点。
中点。
由AD为角平分线,利用角平分线定义得到一对角相等,再由EF与AC平行,利用两直线平行内错角相等得到一对角相等,等量代换可得出∠AEF=∠BAE,利用等角对等边得到AF=EF,再由AE与AD垂直,利用垂直的定义及直角三角形的两锐角互余,得到两对角之和为90°,由∠AEF=∠BAE,利用等角的余角相等可得出∠BEF=∠ABE,利用等角对等边得到BF=EF,等量代换得到AF=BF,即F为AB的中点,得证.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图,在△ABC中CD平分∠ACB,DE∥BC,DE=4,AE=5,则AC=
如图,在△ABC中CD平分∠ACB,DE∥BC,DE=4,AE=5,则AC= 平分
平分 ,交
,交 于点
于点 ,点
,点 在边
在边 上.
上.
 ,那么
,那么 和
和 相等吗?证明你的结论
相等吗?证明你的结论 .
. ,那么
,那么 平分
平分 ,交
,交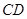 于点
于点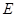 ,点
,点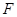 在边
在边 上.
上.
 ,那么
,那么 和
和 相等吗?证明你的结论
相等吗?证明你的结论 .
. ,那么
,那么 平分
平分 ,交
,交 于点
于点 ,点
,点 在边
在边 上.
上.
 ,那么
,那么 和
和 相等吗?证明你的结论.
相等吗?证明你的结论. ,那么
,那么 平分
平分 ,交
,交 于点
于点 ,点
,点 在边
在边 上.
上. ,那么
,那么 和
和 相等吗?证明你的结论.
相等吗?证明你的结论. ,那么
,那么