Question

【题目】问题发现：

（）如图①，已知线段，画出平面内满足的所有点组成的图形．

问题探究：

（）如图②，菱形的对角线与交于点，点、分别是和上的动点，且，点为的中点，已知， ，连接、，求面积的最大值．

问题解决：

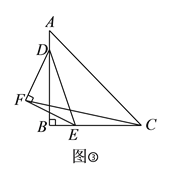
（）如图③，等腰直角三角形的斜边，点、分别是直角边和上的动点，以 为斜边在的左下侧（包括左侧和下侧）作等腰直角三角形，连接，则线段的长度是否存在最小值，若存在，请求出这个最小值；若不存在，请说明理由．

Answer 1

【答案】（）作图见解析（） （）

【解析】试题分析：（1）分别作出以AB为直径的圆和AB的垂直平分线，交点即为所求；

（2）分两种情况讨论即可得出结论.

（3）当连线平行于边时， 顶点与点重合时，则线段的长度是否存在最小值为.

试题解析：（）如图：

①作垂直平分线，交于点．

②以点为圆心， 长为半径作圆．

（）

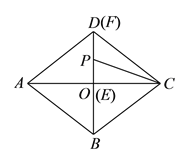
当点在中点点， 点在点时面积最大，

此时，即长．

且点为的中点，如图所示，

连、，如图示，

∴．

（）当连线平行于边时， 顶点与点重合，

∴．