题目内容
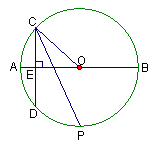
如图,AB为⊙O的直径,弦CD⊥AB于点E.

(1)当AB=10,CD=6时,求OE的长;
(2)∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B点)上移动时,对于点P,下面三个结论:
①到CD的距离保持不变;②平分下半圆;③等分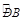 .
.
其中正确的为 ,请予以证明.
【答案】
(1)4(2) ②,证明见解析
【解析】解(1)∵直径AB⊥弦CD,
∴AB平分弦CD,即CE=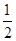 CD=3.………………………………2分
CD=3.………………………………2分
在Rt△OCE中,由勾股定理,
得OE= =
=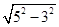 =4;…………………………………4分
=4;…………………………………4分
(2) ② ,………………………………………………………………6分
证明:连结OP(如图2).
 ………………………………………………7分
………………………………………………7分
∵OC=OP,∴∠2=∠3,……………………………………………8分
又∵∠1=∠2,
∴∠1=∠3,
∴CD∥OP.………………………………………………………………9分
∵CD⊥AB,∴OP⊥AB,…………………………………………10分
∴∠AOP=∠BOP=90°,∴ =
= ,……………………12分
,……………………12分
即点P平分下半圆.
(1)由垂径定理求CE,在Rt△OCE中,由勾股定理求OE;
(2)正确的为②,连接OP,利用角平分线的定义得∠1=∠2,由半径OC=OP,得∠2=∠3,从而有∠1=∠3,则OP∥CD,CD⊥AB,则OP⊥AB,即点P平分下半圆.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

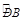 .
.
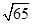 B.3
B.3 C.8 D.2
C.8 D.2