题目内容
在半径为1的⊙O中,弦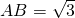 ,
, ,求∠BAC的度数.
,求∠BAC的度数.
解:分两种情况:
(1)当AB、AC在圆心O的同侧时,如图1所示.
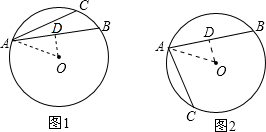
过点O作OD⊥AB于D,连接OA.
∴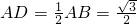 ,OA=1.
,OA=1.
∴ .
.
∴∠OAB=30°.
同理可求:∠OAC=45°.
∴∠BAC=∠OAC-∠OAB=45°-30°=15°.
(2)当AB、AC在圆心O的异侧时,如图2所示.
同理可求:∠OAB=30°,∠OAC=45°.
∴∠BAC=∠OAC+∠OAB=45°+30°=75°.
分析:分两种情况:(1)当AB、AC在圆心O的同侧时,如图1所示.过点O作OD⊥AB于D,连接OA.则求出∠OAB,同理可求:∠OAC,即∠BAC=∠OAC-∠OAB;
(2)当AB、AC在圆心O的异侧时,如图2所示.同理可求:∠OAB和∠OAC.则∠BAC=∠OAC+∠OAB.
点评:本题考查了垂径定理和特殊角的三角函数值,是基础知识要熟练掌握.
(1)当AB、AC在圆心O的同侧时,如图1所示.

过点O作OD⊥AB于D,连接OA.
∴
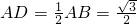 ,OA=1.
,OA=1.∴
 .
.∴∠OAB=30°.
同理可求:∠OAC=45°.
∴∠BAC=∠OAC-∠OAB=45°-30°=15°.
(2)当AB、AC在圆心O的异侧时,如图2所示.
同理可求:∠OAB=30°,∠OAC=45°.
∴∠BAC=∠OAC+∠OAB=45°+30°=75°.
分析:分两种情况:(1)当AB、AC在圆心O的同侧时,如图1所示.过点O作OD⊥AB于D,连接OA.则求出∠OAB,同理可求:∠OAC,即∠BAC=∠OAC-∠OAB;
(2)当AB、AC在圆心O的异侧时,如图2所示.同理可求:∠OAB和∠OAC.则∠BAC=∠OAC+∠OAB.
点评:本题考查了垂径定理和特殊角的三角函数值,是基础知识要熟练掌握.

练习册系列答案
相关题目