题目内容
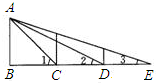 如图,AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3等于( )
如图,AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3等于( )| A、45° | B、60° | C、75° | D、90° |
分析:根据AB=AC,∠B=90°,可以求得∠1=45°,设AB=BC=CD=DE=1,即可求证△ACE∽△DCA,即可求得∠1+∠2+∠3的度数,即可解题.
解答:解:∵AB=BC,∠B=90°,∴∠1=45°.
设AB=BC=CD=DE=1,则AC=
,CE=2,
∴
=
,
=
=
,
∴△ACE∽△DCA,∴∠2=∠CAE.
∵∠1=∠CAE+∠3=∠2+∠3,
∴∠1+∠2+∠3=90°.
故选 D.
设AB=BC=CD=DE=1,则AC=
| 2 |
∴
| CD |
| AC |
| 1 | ||
|
| AC |
| CE |
| ||
| 2 |
| 1 | ||
|
∴△ACE∽△DCA,∴∠2=∠CAE.
∵∠1=∠CAE+∠3=∠2+∠3,
∴∠1+∠2+∠3=90°.
故选 D.
点评:本题考查了相似三角形对应角相等的性质,考查了等腰三角形底角相等的性质,考查了相似三角形的判定,本题中求证∠1=∠CAE+∠3=∠2+∠3是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S=
已知:如图,AB=BC=CA=AD,AH⊥CD于H,CP⊥BC,CP交AH于P.求证:△ABC的面积S= 12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
12、如图,AB=BC=CD,且∠A=15°,则∠ECD=( )
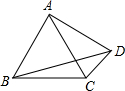 如图,AB=BC=AC=AD,那么∠BDC等于( )
如图,AB=BC=AC=AD,那么∠BDC等于( ) 如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为
如图,AB=BC=CD=DE=1,且BC⊥AB,CD⊥AC,DE⊥AD,则线段AE的长为