题目内容
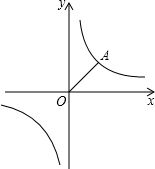 已知反比例函数y=
已知反比例函数y=| k |
| x |
| 1 |
| 2 |
(1)求此反比例函数的解析式;
(2)如图,点A(m,1)是反比例函数图象上的点,求m的值;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使以A、O、P三点为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)将点(-32,-
)代入反比例函数解析式,可得出k的值,继而得出函数解析式;
(2)将点A(m,1)代入(1)所求的解析式可得出m的值;
(3)分情况讨论,①∠APO=90°,②∠OAP'=90°,分别得出点P的坐标即可.
| 1 |
| 2 |
(2)将点A(m,1)代入(1)所求的解析式可得出m的值;
(3)分情况讨论,①∠APO=90°,②∠OAP'=90°,分别得出点P的坐标即可.
解答:解:(1)将点(-32,-
)代入y=
可得:-
=
,
解得:k=16,
故此反比例函数解析式为y=
;
(2)将点A(m,1)代入y=
,可得:1=
,
解得:m=16;
(3)存在点P的坐标.
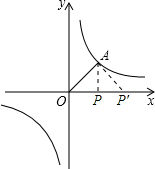
①当∠APO=90°时,OP=16,
此时点P的坐标为(16,0);
②当∠OAP'=90°时,△OAP∽△OP'A,
则
=
,即
=
,
解得:OP'=
,
此时点P'的坐标为(
,0).
综上所述:点P的坐标为(16,0)或(
,0).
| 1 |
| 2 |
| k |
| x |
| 1 |
| 2 |
| k |
| -32 |
解得:k=16,
故此反比例函数解析式为y=
| 16 |
| x |
(2)将点A(m,1)代入y=
| 16 |
| x |
| 16 |
| m |
解得:m=16;
(3)存在点P的坐标.

①当∠APO=90°时,OP=16,
此时点P的坐标为(16,0);
②当∠OAP'=90°时,△OAP∽△OP'A,
则
| OA |
| OP′ |
| OP |
| OA |
| ||
| OP′ |
| 16 | ||
|
解得:OP'=
| 257 |
| 16 |
此时点P'的坐标为(
| 257 |
| 16 |
综上所述:点P的坐标为(16,0)或(
| 257 |
| 16 |
点评:本题属于反比例函数的综合题,涉及了待定系数法求函数解析式、相似三角形的判定与性质及直角三角形的知识,综合性较强,解答本题要求我们熟练各个知识点,并将各知识点融会贯通.

练习册系列答案
相关题目
 面积为3,若直线y=ax+b经过点A,并且经过反比例函数
面积为3,若直线y=ax+b经过点A,并且经过反比例函数 已知反比例函数
已知反比例函数