题目内容
【题目】已知函数y= 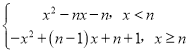 (n为常数)
(n为常数)
(1)若点(3,-7)在函数图象上,求n的值;
(2)当y=1时,求自变量x的值(用含n的代数式表示);
(3)若n-2≤x≤n+1,设函数的最小值为y0.当-5≤y0≤-2时,求n的取值范围;
(4)直接写出函数图象与直线y=-x+4有两个交点时,n的取值范围.
【答案】(1)n=4或n=1;(2)-1或n;(3)1≤n≤-2+2 ![]() ;(4)n≥3或n=-6.
;(4)n≥3或n=-6.
【解析】
(1)分3<n和3≥n两种情况,把(3,-7)分别代入相应的函数关系式,解出n的值即可;
(2)把y=1分别代入两个解析式得到方程并解出x的值,然后要检验解得的x值是否符合条件;
(3)先分别求出当![]() 和
和![]() 时,y的最小值,然后根据两个最小值的大小关系分类讨论,由题意从而可求出n的取值范围;
时,y的最小值,然后根据两个最小值的大小关系分类讨论,由题意从而可求出n的取值范围;
(4)分别求出当x=n时,三个函数的函数值,然后通过比较大小,画出函数的大致图象,结合图象求解即可.
(1)解:当3<n时,将(3,-7)代入y=x-nx-n中,
得-7=3-3n-n,解得n=4.
当3≥n时,将(3,-7)代入y=-x+(n-1)x+n+1中,
得-7=-32+3(n-1)+n+1,解得n=1.
综上,n=4或n=1.
(2)解:当y=x-nx-n=1时,解得x1=-1,x2=n+1,
∵x<n,
∴x1=-1.
当y=-x+(n-1)x+n+1=1时解得x1=-1,x2=n.
综上,y=1时,自变量x的值为-1或n.
(3)解:y= 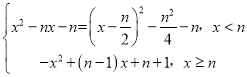
对于![]() ,函数y=
,函数y=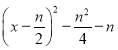 的对称轴为直线x=
的对称轴为直线x=![]() ,开口向上
,开口向上
①当![]() <
<![]() ,即n>4时,
,即n>4时,
此时当![]() 时,y最小=
时,y最小=![]()
由n>4可知: y最小=![]() <-8,显然不符合题意;
<-8,显然不符合题意;
②当![]() ,即0<n≤4时,
,即0<n≤4时,
此时当x=![]() 时, y最小=
时, y最小=![]() ;
;
③当![]() ,即n<0时,
,即n<0时,
此时当![]() 时,y最小=
时,y最小=![]()
由n<0可知: y最小=![]() >0,显然不符合题意;
>0,显然不符合题意;
对于![]() ,函数
,函数![]() 的对称轴为直线x=
的对称轴为直线x=![]() ,开口向小
,开口向小
①当![]() ,即n<-2时,
,即n<-2时,
此时当![]() 时,y最小=
时,y最小=![]() =1,显然不符合题意;
=1,显然不符合题意;
②当![]() ,即n≥-2时,
,即n≥-2时,
此时当![]() 时,y最小=
时,y最小=![]() =-n-1;
=-n-1;
综上:当0<n≤4且![]() <-n-1,即2<n≤4时
<-n-1,即2<n≤4时
-5≤y0=![]() ≤-2
≤-2
解得:![]() 或
或![]()
结合前提条件可得:![]() ;
;
当n≥-2且![]() ≥-n-1,即-2≤n≤2时
≥-n-1,即-2≤n≤2时
-5≤y0=-n-1≤-2
解得:1≤n≤4
结合前提条件可得:1≤n≤2
综上可得:当-5≤y0≤-2时,1≤n![]() ;
;
(4)将x=n代入y=![]() 中,解得:y=
中,解得:y=![]()
将x=n代入y= ![]() 中,解得:y=1
中,解得:y=1
将x=n代入y= ![]() 中,解得:y=-n+4,其中-n+4一定大于
中,解得:y=-n+4,其中-n+4一定大于![]()
当![]() <1,即n>-1时,图象大致如下
<1,即n>-1时,图象大致如下
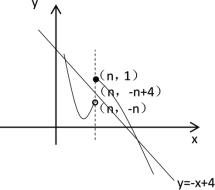
由图可知:当-n≤-n+4≤1时,函数图象与直线y=-x+4有两个交点
解得n≥3;
当![]() ≥1,即n≤-1时,图象大致如下
≥1,即n≤-1时,图象大致如下
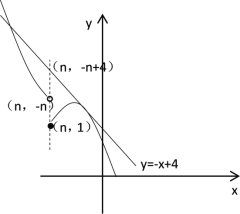
由图可知:当直线y=-x+4与抛物线y= ![]() 有唯一交点时,函数图象y与直线y=-x+4有两个交点
有唯一交点时,函数图象y与直线y=-x+4有两个交点
联立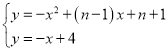
整理,得![]()
由题意可得:![]()
解得:n1=-6,n2=2(不符合前提条件,舍去)
综上:函数图象y与直线y=-x+4有两个交点时,n≥3或n=-6