题目内容
如图,抛物线 与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)

(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点产作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并求出线段MN的最大值;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
 与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
与y轴突于A点,过点A的直线y=kx+l与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点产作PN⊥x轴,交直线AB于点M,交抛物线于点N,设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并求出线段MN的最大值;
(3)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
(1) ;(2)
;(2)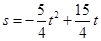 ,
,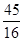 ;(3)当
;(3)当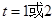 时,四边形BCMN为平行四边形;当
时,四边形BCMN为平行四边形;当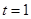 时,平行四边形BCMN为菱形
时,平行四边形BCMN为菱形
 ;(2)
;(2)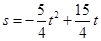 ,
,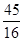 ;(3)当
;(3)当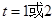 时,四边形BCMN为平行四边形;当
时,四边形BCMN为平行四边形;当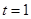 时,平行四边形BCMN为菱形
时,平行四边形BCMN为菱形试题分析:(1)把x=3代入
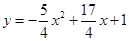 即可求得B点的坐标,再把点B的坐标代入
即可求得B点的坐标,再把点B的坐标代入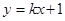 即可求得直线AB的函数关系式;
即可求得直线AB的函数关系式;(2)把x=t分别代入到
 和
和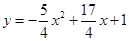 即可得到点M、N的纵坐标,从而可以表示出MN的长,再根据二次函数的性质求解即可;
即可得到点M、N的纵坐标,从而可以表示出MN的长,再根据二次函数的性质求解即可;
(3)在四边形BCMN中,由BC∥MN可知当BC=MN时,四边形BCMN即为平行四边形,即可求得t的值,由勾股定理求得CM的长,再根据菱形的性质求解即可.
(1)把x=3代入
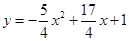 ,得
,得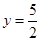 ,
,∴B点的坐标分别(3,
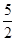 )
)把点B的坐标代入
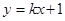 ,得
,得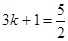 ,解得
,解得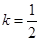
所以
 ;
;(2)把x=t分别代入到
 和
和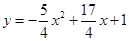
得到点M、N的纵坐标分别为
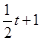 、
、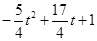
∴MN=
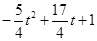 -(
-(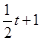 )=
)=

即
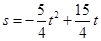 =-
=-
∴MN最大=S最大=
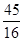 ;
;(3)在四边形BCMN中,∵BC∥MN
∴当BC=MN时,四边形BCMN即为平行四边形
由
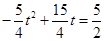 ,得
,得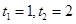
即当
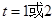 时,四边形BCMN为平行四边形
时,四边形BCMN为平行四边形 当
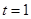 时,PC=2,PM=
时,PC=2,PM=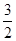 ,由勾股定理求得CM =
,由勾股定理求得CM =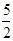
此时BC=CM=
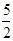 ,平行四边形BCMN为菱形;
,平行四边形BCMN为菱形;当
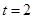 时,PC=1,PM=2,由勾股定理求得CM=
时,PC=1,PM=2,由勾股定理求得CM=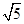
此时BC≠CM,平行四边形BCMN不是菱形;
所以,当
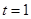 时,平行四边形BCMN为菱形.
时,平行四边形BCMN为菱形.点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目

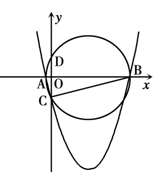
 的图象与
的图象与 轴相交于两个不同的点
轴相交于两个不同的点 、
、 ,与
,与 轴的交点为
轴的交点为 .设
.设 的外接圆的圆心为点
的外接圆的圆心为点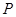 .
.
 与
与 恰好为
恰好为 ,求
,求 和
和 的值.
的值.
 向上平移3单位,得到的抛物线的解析式是____________.
向上平移3单位,得到的抛物线的解析式是____________.
 x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
 的图象如图所示,那么二次函数
的图象如图所示,那么二次函数 的图象大致为( )
的图象大致为( )
