题目内容
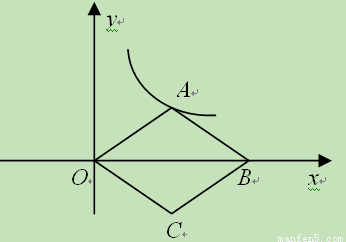
(14分)如图,在坐标系中,菱形ABCD的边BC与x轴重合,点B与原点重合,AB=10,∠ABC=60°.动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动;动点Q从点D出发沿折线DC-CB-BA以每秒3个单位长的速度匀速运动,过点P作PF⊥BC,交折线AB-AC于点E,交直线AD于点F.若P、Q两点同时出发,当其中一点到达终点时整个运动随之停止,设运动时间为t秒.

1.(1)写出点A与点D的坐标
2.(2)当t=3秒时,试判断QE与AB之间的位置关系?
3.(3)当Q在线段DC上运动时,若△PQF为等腰三角形,求t的值;
4.(4)设△PQE的面积为S,求S与t的函数关系式;
1.(1) A(5,![]() ) D(15,
) D(15,![]() )
)
2.(2) 当t=3时,EQ⊥ AB过A作AM//EQ, ∵BP=3时,∠B=60°∴BE=6,∴AE=10-6=4,∴AF=QM=4, ∴DM=3×3-4=5,∴DM=![]() AD,又∵∠ADC=60°,∴∠AMD=90°,∴∠AEQ=90°,∴EQ⊥AB。
AD,又∵∠ADC=60°,∴∠AMD=90°,∴∠AEQ=90°,∴EQ⊥AB。
3.(3)P点坐标为(t,0),F坐标为(t,  ),Q(
),Q(![]() ,
,![]() )
)
(1)当FQ=PQ时,t=![]() (2)当PF=FQ时,
(2)当PF=FQ时,![]() ,∴t1
,∴t1![]() ,t2=5(舍)(3)当PF=PQ时
,t2=5(舍)(3)当PF=PQ时![]() ,∴t1
,∴t1![]() (舍),t2=
(舍),t2=![]() ,∴当t=
,∴当t= ![]() 或
或![]() 或
或![]() 时,△PQF为等腰△。
时,△PQF为等腰△。
4.(4)0∠t≤![]() 时,
时,
S=10×![]() -
-![]()
![]() -
-![]() =-
=-![]() ,
,
![]() <t≤5时,
<t≤5时,
S=![]()
=![]() +
+![]()
5<t<6时,
S=![]()
6<t时≤![]() ,
,
S=![]()
![]() <t≤10,
<t≤10,
S=![]()
=-![]()
解析:略

练习册系列答案
相关题目
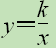 的图象经过点(1,4),菱
的图象经过点(1,4),菱