题目内容

比较大小：
（1）cos89°
＜
＜
cos19°　
（2）cos10°
＞
＞
sin20°．
分析：（1）根据锐角的余弦值是随着角度的增大而减小这一规律解答即可；
（2）先把cos10°转化为sin80°，再根据锐角的正弦值随角度的增大而增大解答即可．
解答：解：（1）∵89°＞19°，
∴cos89°＜cos19°；

（2）∵cos10°=sin（90°-10°）=sin80°，
80°＞20°，
∴sin80°＞sin20°，
即cos10°＞sin20°．
故答案为：＜；＞．
点评：本题考查了锐角三角函数的增减性，锐角三角函数值的变化规律：正弦值和正切值都是随着角度的增大而增大，余弦值和余切值都是随着角度的增大而减小，转化为同名函数是解题的关键．
练习册系列答案
相关题目
如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM=|CE-EO|，再以CM、CO为边作矩形CMNO．
（1）试比较EO、EC的大小，并说明理由；
（2）令m=
S四边形CFGH
S四边形CMNO
，请问m是否为定值？若是，请求出m的值；若不是，请说明理由；
（3）在（2）的条件下，若CO=1，CE=
1
3
，Q为AE上一点且QF=
2
3
，抛物线y=mx2+bx+c经过C、Q两点，请求出此抛物线的解析式；
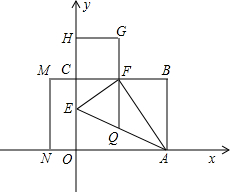（4）在（3）的条件下，若抛物线y=mx2+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△AEF相似？若存在，请求直线KP与y轴的交点T的坐标；若不存在，请说明精英家教网理由．
如图，在?ABCD中，∠B的平分线BE与CD的延长线交于点E．
（1）作出∠C的平分线CO交BE于点O．（要求尺规作图，不写作法，保留作图痕迹）
（2）试比较BO与EO的大小，并说明理由．
如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM=|CE-EO|，再以CM、CO为边作矩形CMNO．
（1）试比较EO、EC的大小，并说明理由；
（2）令m=，请问m是否为定值？若是，请求出m的值；若不是，请说明理由；
（3）在（2）的条件下，若CO=1，CE=，Q为AE上一点且QF=，抛物线y=mx2+bx+c经过C、Q两点，请求出此抛物线的解析式；
（4）在（3）的条件下，若抛物线y=mx2+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△AEF相似？若存在，请求直线KP与y轴的交点T的坐标；若不存在，请说明理由．
如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM=|CE-EO|，再以CM、CO为边作矩形CMNO．
（1）试比较EO、EC的大小，并说明理由；
（2）令m=，请问m是否为定值？若是，请求出m的值；若不是，请说明理由；
（3）在（2）的条件下，若CO=1，CE=，Q为AE上一点且QF=，抛物线y=mx2+bx+c经过C、Q两点，请求出此抛物线的解析式；
（4）在（3）的条件下，若抛物线y=mx2+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△AEF相似？若存在，请求直线KP与y轴的交点T的坐标；若不存在，请说明理由．
如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM=|CE-EO|，再以CM、CO为边作矩形CMNO．
（1）试比较EO、EC的大小，并说明理由；
（2）令m=，请问m是否为定值？若是，请求出m的值；若不是，请说明理由；
（3）在（2）的条件下，若CO=1，CE=，Q为AE上一点且QF=，抛物线y=mx2+bx+c经过C、Q两点，请求出此抛物线的解析式；
（4）在（3）的条件下，若抛物线y=mx2+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△AEF相似？若存在，请求直线KP与y轴的交点T的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网