题目内容
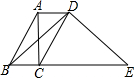如图，平行四边形ABCD中，AC⊥BC，以对角线BD构造等腰△BDE，AD=4cm，CE=12cm，AC=6cm，则DE的长为________．
10cm
分析：过D作DF⊥BE于F，可得DF=AC=6cm，根据平行线的性质可得BC=AD=4cm，求得BE的长度，根据等腰三角形的性质得EF=
BE，然后根据勾股定理求出DE的长度．
解答：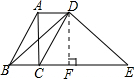
解：过D作DF⊥BE于F，
∵AC⊥BC，
∴DF=AC=6cm，
∵四边形ABCD为平行四边形，
∴BC=AD=4cm，
∴BE=BC+CE=16cm，
∵△BDE为等腰三角形，DF⊥BE，
∴EF=BE=8cm，
∵DF⊥BE，
∴DE=
=10cm．
故答案为：10cm．
点评：本题考查了勾股定理及平行四边形的性质，解答本题的关键是由平行四边形的性质和等腰三角形的性质求得DF、EF的长度，进而利用勾股定理求出斜边的长度．
分析：过D作DF⊥BE于F，可得DF=AC=6cm，根据平行线的性质可得BC=AD=4cm，求得BE的长度，根据等腰三角形的性质得EF=
BE，然后根据勾股定理求出DE的长度．解答：
解：过D作DF⊥BE于F，∵AC⊥BC，
∴DF=AC=6cm，
∵四边形ABCD为平行四边形，
∴BC=AD=4cm，
∴BE=BC+CE=16cm，
∵△BDE为等腰三角形，DF⊥BE，
∴EF=
BE=8cm，∵DF⊥BE，
∴DE=
=10cm．故答案为：10cm．
点评：本题考查了勾股定理及平行四边形的性质，解答本题的关键是由平行四边形的性质和等腰三角形的性质求得DF、EF的长度，进而利用勾股定理求出斜边的长度．
练习册系列答案
相关题目
次方程x2-7x+12=0的两个根，且OA＞OB．
10、如图，平行四边形ABCD中，∠ABC的角平分线BE交AD于E点，AB=3，ED=1，则平行四边形ABCD的周长是
如图，平行四边形ABCD中，对角线AC和BD相交于点O，如果AC=12，BD=10，AB=m，那么m的取值范围是
如图，平行四边形ABCD的两条对角线AC、BD相交于点O，AB=5，AC=6，DB=8，则四边形ABCD是的周长为