题目内容
容积率t是指在房地产开发中建筑面积与用地面积之比,即t=| M建筑面积 | S用地面积 |
(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.
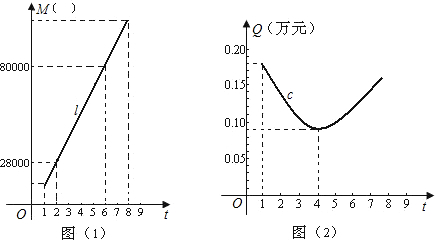
分析:(Ⅰ)因为图象过点(2,28000)和(6,80000),所以易求l的表达式,注意t的取值范围,当t=1时,S用地面积=M建筑面积;根(Ⅱ)据图象经过点(1,0.18)和(4,0.09)且(4,0.09)为顶点可求c的函数关系式.
解答:解:(Ⅰ)设线段l函数关系式为M=kt+b,由图象得
(2分)
解之,得
∴线段l的函数关系式为M=13000t+2000(1≤t≤8). (4分)
由t=
知:
当t=1时,S用地面积=M建筑面积
把t=1代入M=13000t+2000中,
得M=15000 m2.
即开发该小区的用地面积是15000 m2(6分).
(Ⅱ)根据图象特征可设抛物线段c的函数关系式为Q=a(t-4)2+k
把点(4,0.09),(1,0.18)代入,得
(8分)
解之,得
∴抛物线段c的函数关系式为Q=
(t-4)2+
即Q=
t2-
t+
,(1≤t≤8). (10分)
|
解之,得
|
∴线段l的函数关系式为M=13000t+2000(1≤t≤8). (4分)
由t=
| M建筑面积 |
| S用地面积 |
当t=1时,S用地面积=M建筑面积
把t=1代入M=13000t+2000中,
得M=15000 m2.
即开发该小区的用地面积是15000 m2(6分).
(Ⅱ)根据图象特征可设抛物线段c的函数关系式为Q=a(t-4)2+k
把点(4,0.09),(1,0.18)代入,得
|
解之,得
|
∴抛物线段c的函数关系式为Q=
| 1 |
| 100 |
| 9 |
| 100 |
即Q=
| 1 |
| 100 |
| 2 |
| 25 |
| 1 |
| 4 |
点评:根据图象特征求解析式是解决函数问题的基本功,往往就是设合适的解析式,得方程组解之.

练习册系列答案
相关题目
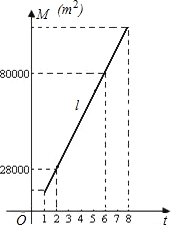 容积率t是指在房地产开发中建筑面积与用地面积之比.为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图中的线段l来表示.
容积率t是指在房地产开发中建筑面积与用地面积之比.为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图中的线段l来表示. ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
 ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
 ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.