题目内容
 6、如图,OC⊥AB,垂足是O,OD⊥OE,那么∠AOD=
6、如图,OC⊥AB,垂足是O,OD⊥OE,那么∠AOD=∠COE
,∠AOD的余角是∠DOC或∠EOB
,∠COD的补角是∠AOE
.分析:由已知OC⊥AB,OD⊥OE,可得∠AOD+∠COD=∠COE+∠COD=90°,从而得∠AOD=∠COE;可根据余角、补角的定义确定∠AOD的余角和∠COD的补角.
解答:解:∵OC⊥AB,OD⊥OE,
∴∠AOD+∠COD=∠COE+∠COD=90°,
∴∠AOD=∠COE;
∵OC⊥AB,OD⊥OE,可得:
∠DOC=∠EOB
∵OC⊥AB,垂足是O,
那么∠AOD的余角是∠DOC或∠EOB;
∠COD即∠EOB的补角是∠AOE.
故答案为:∠COE,∠DOC或∠EOB,∠AOE.
∴∠AOD+∠COD=∠COE+∠COD=90°,
∴∠AOD=∠COE;
∵OC⊥AB,OD⊥OE,可得:
∠DOC=∠EOB
∵OC⊥AB,垂足是O,
那么∠AOD的余角是∠DOC或∠EOB;
∠COD即∠EOB的补角是∠AOE.
故答案为:∠COE,∠DOC或∠EOB,∠AOE.
点评:本题考查垂线及补角、余角的定义,关键是由垂直得∠AOD+∠COD=∠COE+∠COD=90°,及明确:如果两个角的和为180°,则这两个角互为补角;如果两个角的和为90°,则这两个角互为余角.

练习册系列答案
相关题目
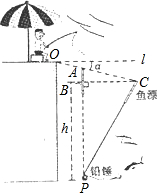 如图所示,张伯伯利用假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6cm,微风吹来,假设铅垂P不动,鱼漂移动了一段距离BC,且顶端恰好与水面齐平,(即PA=PC)水平l与OC的夹角α为8°(点A在OC上),求铅锤P处的水深h.
如图所示,张伯伯利用假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6cm,微风吹来,假设铅垂P不动,鱼漂移动了一段距离BC,且顶端恰好与水面齐平,(即PA=PC)水平l与OC的夹角α为8°(点A在OC上),求铅锤P处的水深h.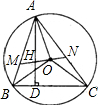 OB、OC,连接OH并延长交AB于M,交AC于N,求证:
OB、OC,连接OH并延长交AB于M,交AC于N,求证: 张开,扣链EF成一条直线,且EF=32cm.
张开,扣链EF成一条直线,且EF=32cm.
