题目内容
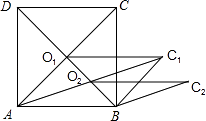
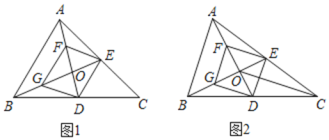
【题目】如图,在![]() 中,点D,E分别是边BC,AC的中点,AD与BE相交于点
中,点D,E分别是边BC,AC的中点,AD与BE相交于点![]() 点F,G分别是线段AO,
点F,G分别是线段AO,
BO的中点.
![]() 求证:四边形DEFG是平行四边形;
求证:四边形DEFG是平行四边形;
![]() 如图2,连接CO,若
如图2,连接CO,若![]() ,求证:四边形DEFG是菱形;
,求证:四边形DEFG是菱形;
![]() 在
在![]() 的前提下,当
的前提下,当![]() 满足什么条件时,四边形DEFG能成为正方形?
满足什么条件时,四边形DEFG能成为正方形?![]() 直接回答即可,不必证明
直接回答即可,不必证明![]()
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)由三角形中位线性质得到![]() ,
,![]() ,故四边形DEFG是平行四边形;(2)同(1),由
,故四边形DEFG是平行四边形;(2)同(1),由![]() ,证
,证![]() ,得到菱形;(3)当
,得到菱形;(3)当![]() 时,四边形DEFG为正方形:点D,E分别是边BC,AC的中点,得点O是
时,四边形DEFG为正方形:点D,E分别是边BC,AC的中点,得点O是![]() 的重心,证
的重心,证![]() ,
,![]() ,结合平行线性质证
,结合平行线性质证![]() ,结合(2)可得结论.
,结合(2)可得结论.
![]() 证明:
证明:![]() 点D,E分别是边BC,AC的中点,
点D,E分别是边BC,AC的中点,![]() ,
,![]() ,
,![]() 点F,G分别是线段AO,BO的中点,
点F,G分别是线段AO,BO的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 四边形DEFG是平行四边形;
四边形DEFG是平行四边形;![]() 证明:
证明:![]() 点F,E分别是边OA,AC的中点,
点F,E分别是边OA,AC的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平行四边形DEFG是菱形;
平行四边形DEFG是菱形;![]() 当
当![]() 时,四边形DEFG为正方形,
时,四边形DEFG为正方形,
理由如下:![]() 点D,E分别是边BC,AC的中点,
点D,E分别是边BC,AC的中点,![]() 点O是
点O是![]() 的重心,
的重心,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 菱形DEFG为正方形.
菱形DEFG为正方形.

练习册系列答案
相关题目