题目内容
如图，在□ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F.
⑴试说明：AB=CF；
⑵连接DE，若AD=2AB，试说明：DE⊥AF.
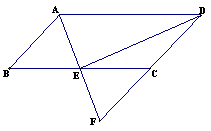
（1）证明：∵四边形ABCD是平行四边形，∴AB‖DF ，
∴∠ABE=∠FCE
∵E为BC中点，∴BE=CE，
在△ABE与△FCE中， ∠ABE=∠FCE； BE=CE ； ∠AEB=∠CEF（对顶角）；
∴△ABE≌△FCE（A.S.A）， ∴AB=FC
（2）∵AD=2AB，AB=FC=CD ∴AD=DF
∵△ABE≌△FCE∴AE=EF
∴DE⊥AF （三线合一）
练习册系列答案
全能测控期末小状元系列答案
智趣暑假温故知新系列答案
相关题目
； 
( x＞0)上，BC与x轴交于点D．若点A的坐标为（1，2），则点B的坐标为_____________________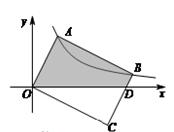
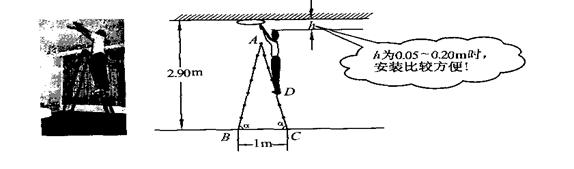
011年至2013年的教育经费投入以相同的百分率逐年增长，该增长率为 ( ) 
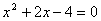B．
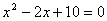
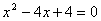D．