题目内容
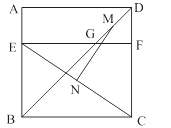
【题目】如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连结DF,M为DF的中点,连结MA,ME.若AM⊥ME,则AE的长为( )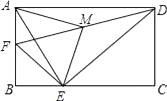
A.5
B.![]()
C.![]()
D.![]()
【答案】B
【解析】设BE=x,则CE=6-x,
∵四边形ABCD矩形,AB=4,
∴AB=CD=4,∠C=∠B=90°,
∴∠DEC+∠CDE=90°,
又∵F是AB的中点,
∴BF=2,
又∵EF⊥ED,
∴∠FED=90°,
∴∠FEB+∠DEC=90°,
∴∠FEB=∠CDE,
∴△BFE∽△CED,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴(x-2)(x-4)=0,
∴x=2,或x=4,
①当x=2时,
∴EF=2![]() ,DE=4
,DE=4![]() ,DF=2
,DF=2![]() ,
,
∴AM=ME=![]() ,
,
∴AE=![]() =
=![]() =2
=2![]() ,
,
②当x=4时,
∴EF=2![]() ,DE=2
,DE=2![]() ,DF=2
,DF=2![]() ,
,
∴AM=ME=![]() ,
,
∴AE=![]() =2
=2![]() ,
,
AE=![]() =4
=4![]() ,
,
∴x=4不合题意,舍去
所以答案是:B.
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目