Question

【题目】在平面直角坐标系xOy中的点Q，我们记点Q到横轴的距离为d1，到纵轴的距离为d2，规定：若d1≥d2，则称d1为点Q的“系长距”；若d1＜d2，则称d2为点Q的“系长距”

例如：点Q（3，﹣4）到横轴的距离d1＝4，到纵轴的距离d2＝3，因为4＞3，所以点Q的系长距”为4

（1）①点A（﹣6，2）的“系长距”为　 　；②若点B（a，2）的“系长距”为4，则a的值为　 　．

（2）已知A（3，0），B（0，4），点P为线段AB上的一点，且PB：PA＝2：3，点P的“系长距”．

（3）若点C在双曲线y＝上，且点C的“系长距”为6，求点C的坐标．

Answer 1

【答案】（1）①6；②±4；（2）；（3）（6， ）或（﹣6，﹣）或（，6）或（﹣，﹣6）．

【解析】

（1）根据“系长距”的定义即可得到结论；
（2）根据勾股定理得到AB=5，过P作PE⊥OA于E，PF⊥OB于F，根据相似三角形的性质得到P（，），根据“系长距”的定义即可得到结论；
（3）设点C的坐标（x，y），由点C的“系长距”为6，得到x=±6或y=±6，分别代入反比例函数的解析式即可得到结论．

解：（1）①∵点A（﹣6，2）到横轴的距离d1＝2，到纵轴的距离d2＝6，因为6＞2，所以点A的“系长距“为：6；

故答案为：6；

②∵点B（a，2）的“系长距”为4，

∴a的值为±4，

故答案为：±4；

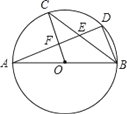
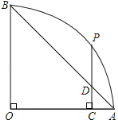
（2）如图，

∵A（3，0），B（0，4），

∴OA＝3，OB＝4，

∴AB＝5，

过P作PE⊥OA于E，PF⊥OB于F，

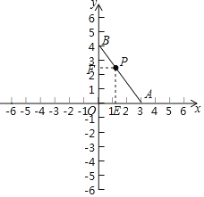
∴PF∥OA，PE∥OB，

∴△PBF∽△BAO，△APE∽△ABO，

∴，，

∵PB：PA＝2：3，

∴PB：AB＝2：5，PA：AB＝3：5，

∴PE＝，PF＝

∴P（，），

∴点P的“系长距”为：；

（3）设点C的坐标（x，y），

∵点C的“系长距”为6，

∴x＝±6或y＝±6，

当x＝6时，y＝，此时点C的坐标为（6，），

当x＝﹣6时，y＝，此时点C的坐标为（﹣6，），

当y＝6时，6＝，x＝，此时点C的坐标为（，6），

当y＝﹣6时，﹣6＝，x＝，此时点C的坐标为（，﹣6），

综上所述，点C的坐标为（6，）或（﹣6，）或（，6）或（，﹣6）．