Question

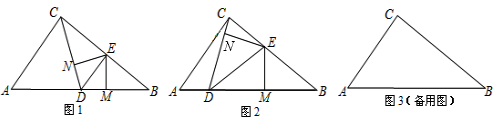
如图①，在Rt△ABC中，已知∠A=90°，AB=AC，G、F分别是AB、AC上的两点，且GF∥BC，AF=2，BG=4。

（1）求梯形BCFG的面积；

（2）有一梯形DEFG与梯形BCFG重合，固定△ABC，将梯形DEFG向右运动，直到点D与点C重合为止，如图②.

 ①若某时段运动后形成的四边形BDG'G中，DG⊥BG'，求运动路程BD的长，并求此时的值；

②设运动中BD的长度为x，试用含x的代数式表示出梯形DEFG与Rt△ABC重合部分的面积S。

 

 

Answer 1

【答案】

(1)16（2）①3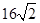2+②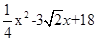

【解析】解：(1)在Rt△ABC中，∵AB＝AC，∴∠ABC＝∠ACB＝45°．又∵GF∥BC，∴∠AGF＝∠AFG=45°．∴AG＝AF＝2，AB＝AC＝6．    ……2分

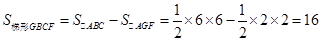    ∴．   ……2分

    (2)①∵在运动过程中有DG′∥BG且DG′＝BG，∴BDG′G是平行四边形．

    当DG⊥BG′时，BDG′G是菱形．∴BD＝BG＝4．    ……2分

    如图③，当BDG′G为菱形时，过点G′作G′M⊥BC于点M．

    在Rt△G′DM中，∠G′DM＝45°，DG′＝4，∴DM＝G′M且．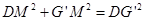

    ∴DM=G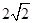′M=，∴BM=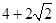．连接G′B．

在Rt△G′BM中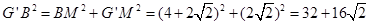，．……2分

    ②当o≤x≤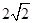时，其重合部分为梯形，如图②．

    在Rt△AGF与Rt△ABC中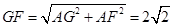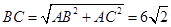，,．过G点作GH垂直BC于点H，得GH=．

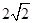    由①，知BD=GG′=x，DC=,．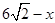

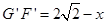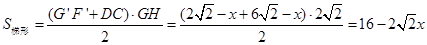    ∴．……1分

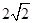      当≤x≤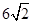时，其重合部分为等腰直角三角形，如图③．

    ∵斜边DC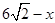＝，斜边上的高为，

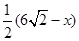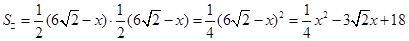   ∴．……1分

（1）在Rt△ABC中由AB=AC得到∠ABC=∠ACB=45°．又由GF∥BC得到∠AGF=∠AFG=45°，由此得到AG=AF=2，AB=AC=6，而S_梯形GBCF=S_△ABC-S_△AGF，所以梯形的面积就可以求出了；

（2）①根据运动过程知道BDG′G是平行四边形，又DG⊥BG′，所以BDG′G是菱形，由此得到BD=BG=4，如图③过点G′作G′M⊥BC于点M，在Rt△G′DM中，∠G′DM=45°，DG′=4可以得到DM=G′M且DM²+G'M²=DG'²，求出DM=G'M= 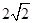，接着得到BM=4+ 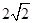，然后在Rt△G′BM中，根据勾股定理可以求出BG'²；②当o≤x≤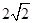时，其重合部分为梯形，如图②．在Rt△AGF与Rt△ABC中分别求出GF，BC，过G点作GH垂直BC于点H，得GH= 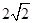，由①知BD=GG′=x，DC= 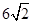-x，G'F'= 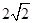-x，现在就可以用x表示S了．当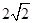≤x≤

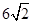
时，其重合部分为等腰直角三角形，如图③．斜边DC=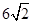 -x，斜边上的高为 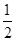(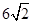-x)，现在也可以用x表示s了．