Question

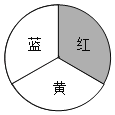
【题目】如图，正方形的顶点、在圆上，若，圆的半径为2，则阴影部分的面积是__________．（结果保留根号和）

Answer 1

【答案】

【解析】

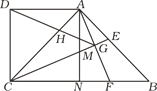
设AD和BC分别与圆交于点E和F，连接AF、OE，过点O作OG⊥AE，根据90°的圆周角对应的弦是直径，可得AF为圆的直径，从而求出AF，然后根据锐角三角函数和勾股定理，即可求出∠AFB和BF，然后根据平行线的性质、锐角三角函数和圆周角定理，即可求出OG、AG和∠EOF，最后利用S阴影=S梯形AFCD－S△AOE－S扇形EOF计算即可．

解：设AD和BC分别与圆交于点E和F，连接AF、OE，过点O作OG⊥AE

∵四边形ABCD是正方形

∴∠ABF=90°，AD∥BC，BC=CD=AD=cm

∴AF为圆的直径

∵，圆的半径为2，

∴AF=4cm

在Rt△ABF中sin∠AFB=，BF=

∴∠AFB=60°，FC=BC－BF=

∴∠EAF=∠AFB=60°

∴∠EOF=2∠EAF=120°

在Rt△AOG中，OG=sin∠EAF·AO=，AG= cos∠EAF·AO=1cm

根据垂径定理，AE=2AG=2cm

∴S阴影=S梯形AFCD－S△AOE－S扇形EOF

=

=

=

故答案为：．