题目内容
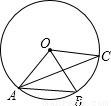
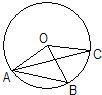6、如图OA、OB、OC都是圆O的半径，∠AOB=2∠BOC．若∠BAC=30°，则∠ACB的度数是（ ）分析：根据圆周角定理，可求得∠BOC=2∠BAC=60°；而∠BOA=2∠BOC=120°，因此A、O、C三点共线，即AC是⊙O的直径，因此∠ABC=90°，由此可求出∠ACB的度数．
解答：解：由圆周角定理知，∠BOC=2∠BAC=60°；
∵∠AOB=2∠BOC=120°，
∴∠AOC=180°，即AC是⊙O的直径；
∴∠ACB=90°-∠CAB=60°．
故选A．
∵∠AOB=2∠BOC=120°，
∴∠AOC=180°，即AC是⊙O的直径；
∴∠ACB=90°-∠CAB=60°．
故选A．
点评：本题考查的是圆周角定理的应用．证得AC是⊙O的直径是解答本题的关键．
练习册系列答案
相关题目
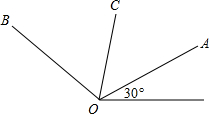如图，线段OB、OC、OA的长度分别是1、2、3，且OC平分∠AOB．若将A点表示为（3，30°），B点表示为（1，120°），则C点可表示为
如图OA、OB、OC都是圆O的半径，∠AOB=2∠BOC．若∠BAC=30°，则∠ACB的度数是
