题目内容
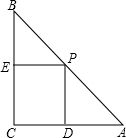 在Rt△ABC中,∠C=90°,AC=BC=4,P是边AB上任意一点(不与点A、点B重合),过P点作PD⊥AC于点D,PE⊥BC于点E.
在Rt△ABC中,∠C=90°,AC=BC=4,P是边AB上任意一点(不与点A、点B重合),过P点作PD⊥AC于点D,PE⊥BC于点E.
(1)求四边形CDPE面积的最大值;
(2)在(1)下所得的四边形CDPE向右平移t个单位,若0≤t≤4,设四边形CDPE与Rt△ABC的重合部分的面积为S,求S与t之间的函数关系式.
解:(1)设PE=x,
∵在Rt△ABC中,∠C=90°,PD⊥AC,PE⊥BC,
∴四边形CDPE是矩形,
∴CD=PE=x,PD∥AC,
∴△ADP∽△PCB,
∴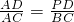 ,
,
∵AC=BC=4,
∴AD=AB-CD=4-x,
∴PD=4-x,
∴S四边形CDPE=PE•PD=x(4-x)=-(x-2)2+4,
∴当pe=2时,四边形CDPE面积的最大,最大值为4;
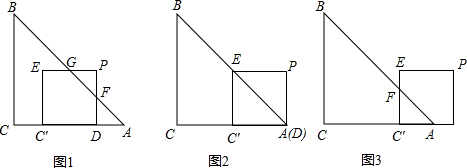 (2)如图1,当0≤t<2时,
(2)如图1,当0≤t<2时,
根据题意得:CC′=t,AD=AC-CC′-C′D=4-2-t=2-t,
∵PE∥AC,
∴△AFD∽△ABC,
∴AD:AC=DF:BC,
∴DF=2-t,
∴PF=PD-DF=t,
∴S△PFG= t2,
t2,
∴S重合部分=S四边形C′DPE-S△PFG=4- t2;
t2;
如图2,当t=2时,点E在AB上时,AC′=EC′=2,
S重合部分=S△AC′E=2;
如图3,当2<t≤4时,AC′=AB-CC′=4-t,
∴C′F=AC′=4-t,
∴S重合部分=S△AC′E= (4-t)2.
(4-t)2.
分析:(1)首先设PE=x,易得四边形CDPE是矩形,又由△ADP∽△PCB,易求得PD的长,继而可得S四边形CDPE=PE•PD=x(4-x)=-(x-2)2+4,则可求得答案;
(2)分别从当0≤t<2时,当t=2时与当2<t≤4时去分析求解即可求得答案.
点评:此题考查了相似三角形的判定与性质、二次函数的最值以及矩形的性质等知识.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.
∵在Rt△ABC中,∠C=90°,PD⊥AC,PE⊥BC,
∴四边形CDPE是矩形,
∴CD=PE=x,PD∥AC,
∴△ADP∽△PCB,
∴
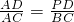 ,
,∵AC=BC=4,
∴AD=AB-CD=4-x,
∴PD=4-x,
∴S四边形CDPE=PE•PD=x(4-x)=-(x-2)2+4,
∴当pe=2时,四边形CDPE面积的最大,最大值为4;
 (2)如图1,当0≤t<2时,
(2)如图1,当0≤t<2时,根据题意得:CC′=t,AD=AC-CC′-C′D=4-2-t=2-t,
∵PE∥AC,
∴△AFD∽△ABC,
∴AD:AC=DF:BC,
∴DF=2-t,
∴PF=PD-DF=t,
∴S△PFG=
 t2,
t2,∴S重合部分=S四边形C′DPE-S△PFG=4-
 t2;
t2;如图2,当t=2时,点E在AB上时,AC′=EC′=2,
S重合部分=S△AC′E=2;
如图3,当2<t≤4时,AC′=AB-CC′=4-t,
∴C′F=AC′=4-t,
∴S重合部分=S△AC′E=
 (4-t)2.
(4-t)2.分析:(1)首先设PE=x,易得四边形CDPE是矩形,又由△ADP∽△PCB,易求得PD的长,继而可得S四边形CDPE=PE•PD=x(4-x)=-(x-2)2+4,则可求得答案;
(2)分别从当0≤t<2时,当t=2时与当2<t≤4时去分析求解即可求得答案.
点评:此题考查了相似三角形的判定与性质、二次函数的最值以及矩形的性质等知识.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )