题目内容
【题目】如图,已知![]() 为直线
为直线![]() 上一点,
上一点,![]() 与
与![]() 互补,
互补,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的平分线,
的平分线,![]() .
.
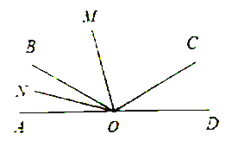
(1)![]() 与
与![]() 相等吗?请说明理由;
相等吗?请说明理由;
(2)求![]() 的度数.
的度数.
【答案】(1)∠COD=∠AOB;(2)18°
【解析】
(1)根据∠AOC+∠COD=180°,∠AOC+∠AOB=180°,即可得到结论;
(2)根据角平分线得到∠AOC=2∠COM =144°,再求得∠AOB=36°,即可求出答案.
(1)∠COD=∠AOB..
理由如下:如图,∵点O在直线AD上,
∴∠AOC+∠COD=180°,
又∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∴∠COD=∠AOB;

(2)∵ OM、ON分别是∠AOC、∠AOB的平分线,
∴∠AOC=2∠COM,∠AON=![]() ∠AOB,
∠AOB,
∵∠MOC=72°,∴∠AOC=2∠COM =144°,
∴∠AOB=∠COD
=180°-∠AOC
=36°,
∴∠AON=![]()
![]() 36°=18°.
36°=18°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目