题目内容
如图,Rt△ABC,∠ABC=90°,圆O与圆M外切,圆O与线段AC、线段BC、线段AB相切于点E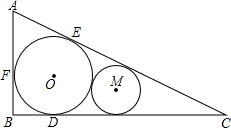 、D、F,圆M与线段AC、线段BC都相切,其中AB=5,BC=12.求:
、D、F,圆M与线段AC、线段BC都相切,其中AB=5,BC=12.求:(1)圆O的半径r;
(2)tg
| C |
| 2 |
(3)sin
| C |
| 2 |
(4)圆M的半径rm.
分析:(1)根据已知条件知道圆O是Rt△ABC的内切圆,根据勾股定理可以求出AC边,然后利用公式即可求出内切圆的半径;
(2)如图(2),连接CO、OD,由于圆O内切于三角形ABC,根据切线的性质可以得到CO平分∠ACB,∠CDO=90°,然后利用三角函数得到tan∠DCO=
=
=
,这样即可求解;
(3)利用(2)的结论和三角函数中正弦的定义即可求解;
(4)由圆M与圆O、线段AC、线段BC都相切得到圆心M必在CO上.过点M作MH⊥OD,如图3,所以MH∥CD,根据平行线的性质得到∠OMH=∠DCO,接着得到sin∠OMH=
=sin∠DCO=
,由此得到关于rm的方程,解方程即可求解.
(2)如图(2),连接CO、OD,由于圆O内切于三角形ABC,根据切线的性质可以得到CO平分∠ACB,∠CDO=90°,然后利用三角函数得到tan∠DCO=
| r |
| CD |
| 2 |
| 12-2 |
| 1 |
| 5 |
(3)利用(2)的结论和三角函数中正弦的定义即可求解;
(4)由圆M与圆O、线段AC、线段BC都相切得到圆心M必在CO上.过点M作MH⊥OD,如图3,所以MH∥CD,根据平行线的性质得到∠OMH=∠DCO,接着得到sin∠OMH=
| OH |
| OM |
| ||
| 26 |
解答: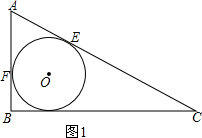 解:
解:
(1)如图1,
∵∠B=90°,
c=5,a=12,
∴b=13.(1分)
r=
=
=2.
(2)在图2中,连接CO、OD,
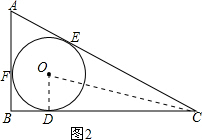 ∵圆O内切于三角形ABC,
∵圆O内切于三角形ABC,
∴CO平分∠ACB,∠CDO=90°.(2分)
tan∠DCO=
=
=
.(1分)
(3)sin∠DCO=
=
=
.(2分)
(4)∵圆M与圆O、线段AC、线段BC都相切,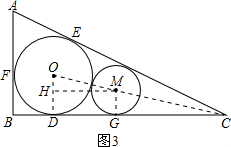
∴圆心M必在CO上.
过点M作MH⊥OD,如图3,
∴MH∥CD,(1分)
∴∠OMH=∠DCO.
∴sin∠OMH=
=sin∠DCO=
,
∴
=
,即
=
,(2分)
解得rM=
.(1分)
 解:
解:(1)如图1,
∵∠B=90°,
c=5,a=12,
∴b=13.(1分)
r=
| a+c-b |
| 2 |
| 12+5-13 |
| 2 |
(2)在图2中,连接CO、OD,
 ∵圆O内切于三角形ABC,
∵圆O内切于三角形ABC,∴CO平分∠ACB,∠CDO=90°.(2分)
tan∠DCO=
| r |
| CD |
| 2 |
| 12-2 |
| 1 |
| 5 |
(3)sin∠DCO=
| r |
| CO |
| 2 | ||
|
| ||
| 26 |
(4)∵圆M与圆O、线段AC、线段BC都相切,

∴圆心M必在CO上.
过点M作MH⊥OD,如图3,
∴MH∥CD,(1分)
∴∠OMH=∠DCO.
∴sin∠OMH=
| OH |
| OM |
| ||
| 26 |
∴
| r-rM |
| r+rM |
| 1 | ||
|
| 2-rM |
| 2+rM |
| 1 | ||
|
解得rM=
54-4
| ||
| 25 |
点评:此题主要考查了相切两圆的性质及解直角三角形,有一定的综合性,解题时首先利用直角三角形内切圆的知识求出半径,然后利用相切两圆的性质和三角函数的定义即可求解.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过
如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过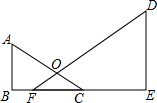 已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15.
已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15. (2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6
(2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6