Question

【题目】如图，正方形ABCD中，点G是边CD上一点（不与端点C，D重合），以CG为边在正方形ABCD外作正方形CEFG，且B、C、E三点在同一直线上，设正方形ABCD和正方形CEFG的边长分别为a和b．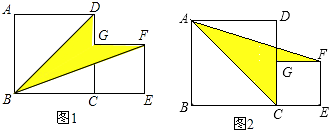

（1）分别用含a，b的代数式表示图1和图2中阴影部分的面积S1、S2；
（2）如果a+b=5，ab=3，求S1的值；
（3）当S1＜S2时，求 的取值范围．

Answer 1

【答案】
（1）解：S1=a2+b2﹣ a2﹣ b（a+b）

= a2+ b2﹣ ab，

S2=a（a+b）﹣b2﹣ a2﹣ （a﹣b）（a+b）

=ab﹣ b2．

（2）解：∵a+b=5，ab=3，

∴S1= a2+ b2﹣ ab

= （a+b）2﹣ ab= ﹣ =8

（3）解：∵ a2+ b2﹣ ab＜ab﹣ b2．

∴ a2+b2﹣ ab＜0，

∴a2+2b2﹣3ab＜0，

∴（a﹣2b）（a﹣b）＜0，

∵a＞b，

∴a﹣2b＜0，

∴a＜2b，

∴1＜ ＜2

【解析】（1）利用两个正方形的面积减去空白部分的面积列式即可；（2）把a+b=5，ab=3，整体代入S1的代数式求得数值即可；（3）联立不等式，进一步求得答案即可．
【考点精析】解答此题的关键在于理解代数式求值的相关知识，掌握求代数式的值，一般是先将代数式化简，然后再将字母的取值代入；求代数式的值，有时求不出其字母的值，需要利用技巧，“整体”代入，以及对因式分解的应用的理解，了解因式分解是整式乘法的逆向变形，可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程．