题目内容
 甲乙两个工程队分别从A,B两村同时相向开始修筑公路,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通,甲乙两个工程队修道路的长度y(米)与修筑时间x(天)之间的函数图象如图,则该公路的总长度为________米.
甲乙两个工程队分别从A,B两村同时相向开始修筑公路,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通,甲乙两个工程队修道路的长度y(米)与修筑时间x(天)之间的函数图象如图,则该公路的总长度为________米.
1800
分析:先求乙修筑时间与修道路长度的函数关系式,求出x=8时的函数值,利用“两点法”求甲当4≤x≤16时的函数关系式,令x=16,求甲修道路的长度,得出甲、乙修道路的总长度.
解答:设乙修道路的长度y(米)与修筑时间x(天)之间的函数关系式为y=ax,
将点(12,840)代入,得12a=840,解得a=70,
∴y=70x,当x=8时,y=70×8=560,
当4≤x≤16时,设甲修道路的长度y(米)与修筑时间x(天)之间的函数关系式为y=mx+n,
将点(4,360),(8,560)代入,得 ,解得
,解得 ,
,
∴y=50x+160,当x=16时,y=50×16+160=960,
该公路总长度为:960+840=1800米.
故答案为:1800.
点评:本题考查了一次函数的运用.关键是结合函数图象求函数关系式,运用函数关系式求甲、乙修道路的长度.
分析:先求乙修筑时间与修道路长度的函数关系式,求出x=8时的函数值,利用“两点法”求甲当4≤x≤16时的函数关系式,令x=16,求甲修道路的长度,得出甲、乙修道路的总长度.
解答:设乙修道路的长度y(米)与修筑时间x(天)之间的函数关系式为y=ax,
将点(12,840)代入,得12a=840,解得a=70,
∴y=70x,当x=8时,y=70×8=560,
当4≤x≤16时,设甲修道路的长度y(米)与修筑时间x(天)之间的函数关系式为y=mx+n,
将点(4,360),(8,560)代入,得
 ,解得
,解得 ,
,∴y=50x+160,当x=16时,y=50×16+160=960,
该公路总长度为:960+840=1800米.
故答案为:1800.
点评:本题考查了一次函数的运用.关键是结合函数图象求函数关系式,运用函数关系式求甲、乙修道路的长度.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
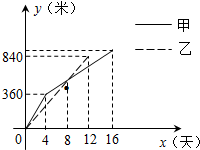 甲乙两个工程队分别从A,B两村同时相向开始修筑公路,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通,甲乙两个工程队修道路的长度y(米)与修筑时间x(天)之间的函数图象如图,则该公路的总长度为
甲乙两个工程队分别从A,B两村同时相向开始修筑公路,施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通,甲乙两个工程队修道路的长度y(米)与修筑时间x(天)之间的函数图象如图,则该公路的总长度为
