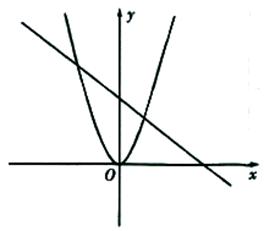
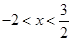题目内容
如图,已知平面直角坐标系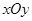 中,点
中,点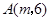 ,
,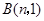 为两动点,其中
为两动点,其中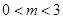 ,连结
,连结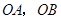 ,
,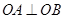 .
.
(1)求证: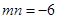 ;
;
(2)当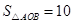 时,抛物线经过
时,抛物线经过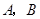 两点且以
两点且以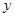 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;
(3)在(2)的条件下,设直线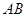 交
交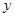 轴于点
轴于点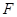 ,过点
,过点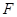 作直线
作直线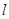 交抛物线于
交抛物线于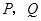 两点,问是否存在直线
两点,问是否存在直线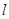 ,使
,使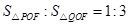 ?若存在,求出直线
?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.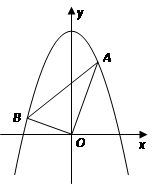
 中,点
中,点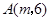 ,
,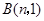 为两动点,其中
为两动点,其中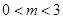 ,连结
,连结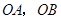 ,
,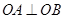 .
.(1)求证:
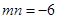 ;
;(2)当
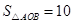 时,抛物线经过
时,抛物线经过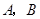 两点且以
两点且以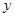 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;(3)在(2)的条件下,设直线
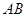 交
交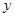 轴于点
轴于点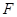 ,过点
,过点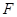 作直线
作直线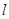 交抛物线于
交抛物线于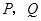 两点,问是否存在直线
两点,问是否存在直线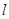 ,使
,使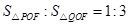 ?若存在,求出直线
?若存在,求出直线 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.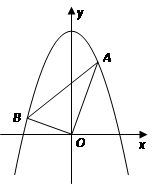
(1)作 轴于
轴于 点,
点,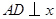 轴于
轴于 点,
点,
 点坐标分别为
点坐标分别为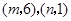 ,
,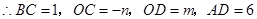 ,
,
又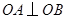 ,易证
,易证 ,
,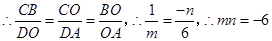 .
.
(2)由(1)得,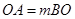 ,又
,又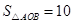 ,
,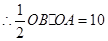 ,
,
即 .又
.又
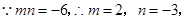
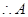 坐标为
坐标为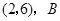 坐标为
坐标为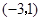 ,
,
易得抛物线解析式为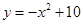 .
.
(3)直线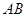 为
为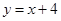 ,且与
,且与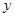 轴交于
轴交于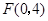 点,
点,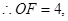
假设存在直线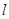 交抛物线于
交抛物线于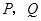 两点,且使
两点,且使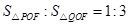 ,如图所示,
,如图所示,
则有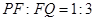 ,作
,作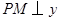 轴于
轴于 点,
点, 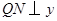 轴于
轴于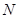 点,
点,

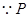 在抛物线
在抛物线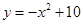 上,
上, 设
设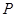 坐标为
坐标为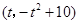 ,
,
则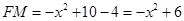 ,易证
,易证 ,
,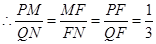 ,
,
 ,
, ,
,
 点坐标为
点坐标为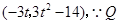 点在抛物线
点在抛物线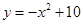 上,
上,
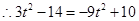 ,解得
,解得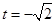 ,
,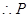 坐标为
坐标为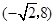 ,
,
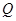 坐标为
坐标为 ,
,
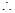 易得直线
易得直线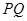 为
为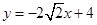 .
.
根据抛物线的对称性可得直线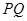 另解为
另解为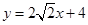 .
.
 轴于
轴于 点,
点, 轴于
轴于 点,
点, 点坐标分别为
点坐标分别为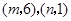 ,
,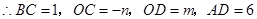 ,
,又
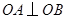 ,易证
,易证 ,
,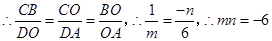 .
.(2)由(1)得,
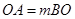 ,又
,又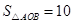 ,
,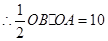 ,
,即
 .又
.又
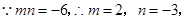
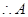 坐标为
坐标为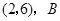 坐标为
坐标为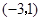 ,
,易得抛物线解析式为
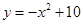 .
.(3)直线
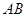 为
为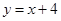 ,且与
,且与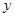 轴交于
轴交于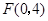 点,
点,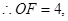
假设存在直线
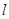 交抛物线于
交抛物线于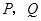 两点,且使
两点,且使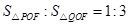 ,如图所示,
,如图所示,则有
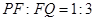 ,作
,作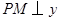 轴于
轴于 点,
点, 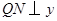 轴于
轴于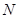 点,
点,
 在抛物线
在抛物线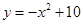 上,
上, 设
设 坐标为
坐标为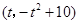 ,
,则
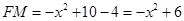 ,易证
,易证 ,
,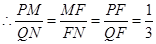 ,
, ,
, ,
, 点坐标为
点坐标为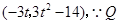 点在抛物线
点在抛物线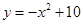 上,
上,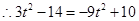 ,解得
,解得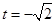 ,
, 坐标为
坐标为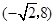 ,
,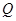 坐标为
坐标为 ,
,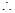 易得直线
易得直线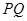 为
为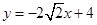 .
.根据抛物线的对称性可得直线
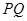 另解为
另解为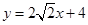 .
.(1)作BC⊥x轴于C点,AD⊥x轴于D点.因为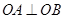 ,可得∠BOC+∠AOD=90°.因为BC⊥x,所以易证∠∠AOD=∠OBC,从而得△CBO∽△DOA,利用线段比求出mn.
,可得∠BOC+∠AOD=90°.因为BC⊥x,所以易证∠∠AOD=∠OBC,从而得△CBO∽△DOA,利用线段比求出mn.
(2)由(1)得m与BO的关系式,根据勾股定理得BO与n的关系式,从而建立m与n的一个关系式,然后利用(1)中mn=-6,求得m、n的值.然后得A,B的坐标以及抛物线解析式.
(3)利用待定系数法求出直线AB解析式,从而求出F点的坐标.过作PM⊥y轴于M点,QN⊥y轴于N点,根据同底等高的三角形面积比等于高的比得PM:QN=1:3.易证△PMF∽△QNF,设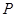 坐标为
坐标为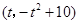 ,易得QN、NF、ON的长,进而表示出点Q的坐标.因为点Q在二次函数上,所以求得t的值.从而得直线
,易得QN、NF、ON的长,进而表示出点Q的坐标.因为点Q在二次函数上,所以求得t的值.从而得直线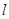 的解析式,根据对称性得到第二条直线
的解析式,根据对称性得到第二条直线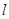 的解析式.
的解析式.
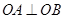 ,可得∠BOC+∠AOD=90°.因为BC⊥x,所以易证∠∠AOD=∠OBC,从而得△CBO∽△DOA,利用线段比求出mn.
,可得∠BOC+∠AOD=90°.因为BC⊥x,所以易证∠∠AOD=∠OBC,从而得△CBO∽△DOA,利用线段比求出mn.(2)由(1)得m与BO的关系式,根据勾股定理得BO与n的关系式,从而建立m与n的一个关系式,然后利用(1)中mn=-6,求得m、n的值.然后得A,B的坐标以及抛物线解析式.
(3)利用待定系数法求出直线AB解析式,从而求出F点的坐标.过作PM⊥y轴于M点,QN⊥y轴于N点,根据同底等高的三角形面积比等于高的比得PM:QN=1:3.易证△PMF∽△QNF,设
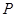 坐标为
坐标为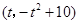 ,易得QN、NF、ON的长,进而表示出点Q的坐标.因为点Q在二次函数上,所以求得t的值.从而得直线
,易得QN、NF、ON的长,进而表示出点Q的坐标.因为点Q在二次函数上,所以求得t的值.从而得直线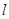 的解析式,根据对称性得到第二条直线
的解析式,根据对称性得到第二条直线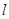 的解析式.
的解析式.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
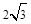 ,0)作圆B的切线交圆于点P,已知tan∠PAB=
,0)作圆B的切线交圆于点P,已知tan∠PAB=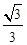 ,抛物线C经过A、P两点。
,抛物线C经过A、P两点。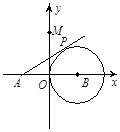
 ,
, 的点共有 个;
的点共有 个;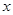 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量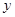 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间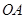 是抛物线的一部分,
是抛物线的一部分,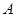 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
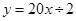

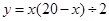
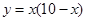
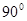 ,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
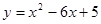 的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线
的部分图象如图,则抛物线的对称轴为直线x= ,满足y<0的x的取值范围是 ,将抛物线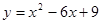 .
.
 与函数
与函数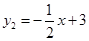 的图象大致如图.若
的图象大致如图.若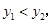 则自变量
则自变量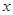 的取值范围是( ).
的取值范围是( ).