题目内容
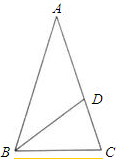如图，等腰△ABC中，∠A=36°，AB=AC=a，D在AC上，且∠DBC=36°，试求BD的长（精确到0.001a）．
解：∵∠A=∠DBC=36°，∠C公共，∴△ABC∽△BDC，
且AD=BD=BC．
设BD=x，则BC=x，CD=a-x．
由于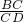
=
，∴
=
．
整理得：x2+ax-a2=0
解方程得：x=
∵x为正数，∴x=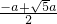
≈0.618a．
所以BD的长为0.618a．
分析：根据两角对应相等，判定两个三角形相似．再用相似三角形对应边的比相等进行计算求出BD的长．
点评：本题考查的是相似三角形的判定与性质，先用两角对应相等判定两个三角形相似，再用相似三角形的性质对应边的比相等进行计算求出BD的长．
且AD=BD=BC．
设BD=x，则BC=x，CD=a-x．
由于
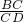=，∴=．整理得：x2+ax-a2=0
解方程得：x=
∵x为正数，∴x=
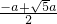≈0.618a．所以BD的长为0.618a．
分析：根据两角对应相等，判定两个三角形相似．再用相似三角形对应边的比相等进行计算求出BD的长．
点评：本题考查的是相似三角形的判定与性质，先用两角对应相等判定两个三角形相似，再用相似三角形的性质对应边的比相等进行计算求出BD的长．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
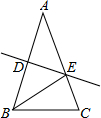如图，等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）| A、80° | B、70° | C、60° | D、50° |
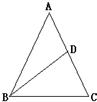13、如图，等腰△ABC中，AB=AC，BD为腰AC的中线，将△ABC分成长12cm和9cm的两段，则等腰△ABC的腰长为
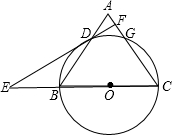如图，等腰△ABC中，AC=BC=10，AB=12，以BC为直径作⊙0交AB于D，交AC于G，DF⊥AC，垂足为F，交CB的延长线于点E，则sinE=
如图，等腰△ABC中，AB=AC，D为BC中点，E为射线AD上一点．
如图，等腰△ABC中，AB=AC，D、E分别为AC、AB的中点．