题目内容
如图，△ABC是等腰直角三角形，∠ABC=90°，AB=10，D为△ABC外一点，连接AD、BD，过D作DH⊥AB，垂足为H，交AC于E，若BD=AB，且tan∠HDB=
，则DE=________．
4
分析：首先利用锐角三角函数的定义，求得BH，进一步求出AH，再证明△AEH∽△ACB，利用相似三角形的性质解决问题．
解答：因DB=AB=10，tan∠HDB=BH：DH=3：4，
又∵DH⊥AB，△DBH为直角三角形，
∴DH=8，HB=6；
AH=AB-BH=10-6=4，
∵∠ABC=90°，
∴DH∥BC，
∴△AEH∽△ACB，
∴
=
，
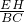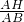即EH=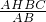
=4，
∴DE=DH-EH=4．
故答案为4．
点评：此题主要考查锐角三角函数的定义，三角形相似的判定与性质，线段的和与差等知识点，属于基础题．
分析：首先利用锐角三角函数的定义，求得BH，进一步求出AH，再证明△AEH∽△ACB，利用相似三角形的性质解决问题．
解答：因DB=AB=10，tan∠HDB=BH：DH=3：4，
又∵DH⊥AB，△DBH为直角三角形，
∴DH=8，HB=6；
AH=AB-BH=10-6=4，
∵∠ABC=90°，
∴DH∥BC，
∴△AEH∽△ACB，
∴
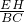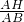=，即EH=
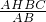=4，∴DE=DH-EH=4．
故答案为4．
点评：此题主要考查锐角三角函数的定义，三角形相似的判定与性质，线段的和与差等知识点，属于基础题．
练习册系列答案
一课一练课时达标系列答案
相关题目
如图，△ABC是等腰直角三角形，BC是斜边，点P是△ABC内一定点，延长BP至P′，将△ABP绕点A旋转后，与△ACP′重合，如果AP=
如图，△ABC是等腰直角三角形，∠ACB=90°，BC=AC，把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′，若AB=2，则线段BC在上述旋转过程中所扫过部分（阴影部分）的面积是
（2012•资阳）如图，△ABC是等腰三角形，点D是底边BC上异于BC中点的一个点，∠ADE=∠DAC，DE=AC．运用这个图（不添加辅助线）可以说明下列哪一个命题是假命题？（ ）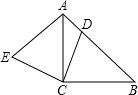
已知：如图，△ABC是等腰直角三角形，D为斜边AB上任意一点（不与A，B重合），连接CD，作EC⊥DC，且EC=DC，连接AE．