题目内容
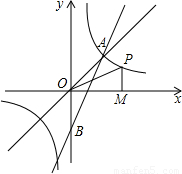
(2009•赣州二模)如图:P是反比例函数y= (k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,已知△POM的面积为2.
(k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,已知△POM的面积为2.(1)求k的值;
(2)若直线y=x与反比例函数y=
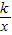 的图象在第一象限内交于点A,求过点A和点B(0,-2)的直线表达式;
的图象在第一象限内交于点A,求过点A和点B(0,-2)的直线表达式;(3)过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
【答案】分析:(1)设出点P的坐标,用它表示出三角形的面积,反比例函数的比例系数=这点横纵坐标的积;
(2)让正比例函数和反比例函数组成方程组求出在第一象限的交点A,把A,B两点代入一次函数解析式即可;
(3)直角相等是固定的,当另两对角的对应是不固定的,所以应分两种情况进行讨论.
解答: 解:(1)∵△POM的面积为2,
解:(1)∵△POM的面积为2,
设P(x,y),
∴ xy=2,即xy=4,
xy=2,即xy=4,
∴k=4;
(2)解方程组 ,得
,得 ,或
,或 ,
,
∵点A在第一象限,
∴A(2,2),(3分)
设直线AB的表达式为y=mx+n,
将A(2,2)B(0,-2)代入得: 解之得
解之得 ,
,
∴直线AB的表达式为y=2x-2;
(3)①若△ABC∽△POM,则有PM:OM=AC:AB=2:4=1:2,
又 PM•OM=2,即
PM•OM=2,即 ×2PM•PM=2,得PM=
×2PM•PM=2,得PM= ∴P(2
∴P(2 ,
, );
);
②若△ABC∽△OPM,同上述方法,易得OM= ,∴P(
,∴P( ,2
,2 ),
),
∴符合条件的点P有(2 ,
, )或(
)或( ,2
,2 ).(9分)
).(9分)
点评:反比例函数的比例系数等于它上面的点的横纵坐标的积;求一次函数的解析式需知道它上面的两个点的坐标;当没有给出相似三角形的对应顶点时,需注意分情况探讨.
(2)让正比例函数和反比例函数组成方程组求出在第一象限的交点A,把A,B两点代入一次函数解析式即可;
(3)直角相等是固定的,当另两对角的对应是不固定的,所以应分两种情况进行讨论.
解答:
 解:(1)∵△POM的面积为2,
解:(1)∵△POM的面积为2,设P(x,y),
∴
 xy=2,即xy=4,
xy=2,即xy=4,∴k=4;
(2)解方程组
 ,得
,得 ,或
,或 ,
,∵点A在第一象限,
∴A(2,2),(3分)
设直线AB的表达式为y=mx+n,
将A(2,2)B(0,-2)代入得:
 解之得
解之得 ,
,∴直线AB的表达式为y=2x-2;
(3)①若△ABC∽△POM,则有PM:OM=AC:AB=2:4=1:2,
又
 PM•OM=2,即
PM•OM=2,即 ×2PM•PM=2,得PM=
×2PM•PM=2,得PM= ∴P(2
∴P(2 ,
, );
);②若△ABC∽△OPM,同上述方法,易得OM=
 ,∴P(
,∴P( ,2
,2 ),
),∴符合条件的点P有(2
 ,
, )或(
)或( ,2
,2 ).(9分)
).(9分)点评:反比例函数的比例系数等于它上面的点的横纵坐标的积;求一次函数的解析式需知道它上面的两个点的坐标;当没有给出相似三角形的对应顶点时,需注意分情况探讨.

练习册系列答案
相关题目

