Question

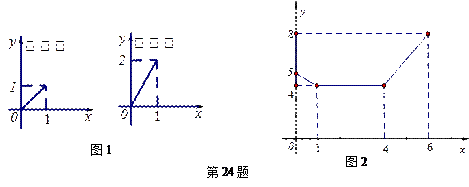
一个安装了两个进水管和一个出水管的容器，每分钟的进水量和出水量是两个常数，且两个进水管的进水速度相同. 进水管和出水管的进出水速度如图1所示，某时刻开始到6分钟（至少打开一个水管），该容器的水量y（单位：升）与时间x（单位：分）如图2所示.。

（1）试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况。
（2）求4≤x≤6时，y随x变化的函数关系式.。
（3）6分钟后，若同时打开两个水管，则10分钟时容器的水量是多少升？

Answer 1

解：（1） 0到1分，打开一个进水管， 打开一个出水管 1分到4分，两个进水管和一个出水管全部打开 4分到6分，打开两个进水管，关闭出水管。
（2）当4≤x≤6时，函数图象过点（4，4）（6，8）；
设解析式为y=kx+b，依题意得：；
解得。
∴函数解析式为y=2x-4
（3）若同时打开一个进水管，一个出水管，则10分钟时容器的水量是8+（-1）×4=4升 ，
若同时打开两个进水管，则10分钟时容器的水量是8+2×4=16升。