题目内容
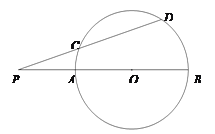
【题目】已知P是![]() 的直径BA延长线上的一个动点,∠P的另一边交
的直径BA延长线上的一个动点,∠P的另一边交![]() 于点C、D,两点位于AB的上方,
于点C、D,两点位于AB的上方,![]() =6,OP=m,
=6,OP=m,![]() ,如图所示.另一个半径为6的
,如图所示.另一个半径为6的![]() 经过点C、D,圆心距
经过点C、D,圆心距![]() .
.
(1)当m=6时,求线段CD的长;
(2)设圆心O1在直线![]() 上方,试用n的代数式表示m;
上方,试用n的代数式表示m;
(3)△POO1在点P的运动过程中,是否能成为以OO1为腰的等腰三角形,如果能,试求出此时n的值;如果不能,请说明理由.
【答案】(1)CD=![]() ;(2)m=
;(2)m=![]() ;(3) n的值为
;(3) n的值为![]() 或
或![]()
【解析】分析:(1)过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .解Rt△
.解Rt△![]() ,得到
,得到![]() 的长.由勾股定理得
的长.由勾股定理得![]() 的长,再由垂径定理即可得到结论;
的长,再由垂径定理即可得到结论;
(2)解Rt△![]() ,得到
,得到![]() 和Rt△
和Rt△![]() 中,由勾股定理即可得到结论;
中,由勾股定理即可得到结论;
(3)△![]() 成为等腰三角形可分以下几种情况讨论:① 当圆心
成为等腰三角形可分以下几种情况讨论:① 当圆心![]() 、
、![]() 在弦
在弦![]() 异侧时,分
异侧时,分![]() 和
和![]() .②当圆心
.②当圆心![]() 、
、![]() 在弦
在弦![]() 同侧时,同理可得结论.
同侧时,同理可得结论.
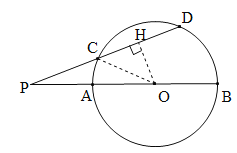
详解:(1)过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
在Rt△![]() ,∴
,∴![]() .
.
∵![]() =6,∴
=6,∴![]() .
.
由勾股定理得: ![]() .
.
∵![]() ⊥
⊥![]() ,∴
,∴![]() .
.
(2)在Rt△![]() ,∴
,∴![]() .
.
在Rt△![]() 中,
中,![]() .
.
在Rt△![]() 中,
中,![]() .
.
可得: ![]() ,解得
,解得![]() .
.
(3)△![]() 成为等腰三角形可分以下几种情况:
成为等腰三角形可分以下几种情况:
① 当圆心![]() 、
、![]() 在弦
在弦![]() 异侧时
异侧时
i)![]() ,即
,即![]() ,由
,由![]() ,解得
,解得![]() .
.
即圆心距等于![]() 、
、![]() 的半径的和,就有
的半径的和,就有![]() 、
、![]() 外切不合题意舍去.
外切不合题意舍去.
ii)![]() ,由
,由![]()
![]() ,
,
解得:![]() ,即
,即![]()
![]() ,解得
,解得![]() .
.
②当圆心![]() 、
、![]() 在弦
在弦![]() 同侧时,同理可得:
同侧时,同理可得: ![]() .
.
∵![]() 是钝角,∴只能是
是钝角,∴只能是![]() ,即
,即![]() ,解得
,解得![]() .
.
综上所述:n的值为![]() 或
或![]() .
.

练习册系列答案
相关题目