题目内容
如图，等腰△ABC中，AB=AC=7cm，BC=3cm，E、D分别是AB、AC上的点，BD平分∠ABC，ED∥BC，则ED=________cm．
2.1
分析：根据BD平分∠ABC，ED∥BC，易证ED=BE，△AED∽△ABC，根据相似三角形的对应边的比相等，即可求得ED的长．
解答：∵ED∥BC，
∴∠EDB=∠DBC，
又∵∠EBD=∠DBC，
∴∠EBD=∠EDB，
∴BE=ED．
设ED=x，则BE=x，AE=7-x．
∵ED∥BC，
∴△AED∽△ABC．
∴
=
，
∴
=
，
解得x=2.1，
即ED=2.1cm．
故答案为2.1．
点评：本题主要考查了相似三角形的性质，相似三角形对应边的比相等．
分析：根据BD平分∠ABC，ED∥BC，易证ED=BE，△AED∽△ABC，根据相似三角形的对应边的比相等，即可求得ED的长．
解答：∵ED∥BC，
∴∠EDB=∠DBC，
又∵∠EBD=∠DBC，
∴∠EBD=∠EDB，
∴BE=ED．
设ED=x，则BE=x，AE=7-x．
∵ED∥BC，
∴△AED∽△ABC．
∴
=，∴
=，解得x=2.1，
即ED=2.1cm．
故答案为2.1．
点评：本题主要考查了相似三角形的性质，相似三角形对应边的比相等．
练习册系列答案
相关题目
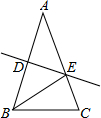如图，等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）| A、80° | B、70° | C、60° | D、50° |
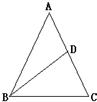13、如图，等腰△ABC中，AB=AC，BD为腰AC的中线，将△ABC分成长12cm和9cm的两段，则等腰△ABC的腰长为
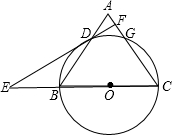如图，等腰△ABC中，AC=BC=10，AB=12，以BC为直径作⊙0交AB于D，交AC于G，DF⊥AC，垂足为F，交CB的延长线于点E，则sinE=
如图，等腰△ABC中，AB=AC，D为BC中点，E为射线AD上一点．
如图，等腰△ABC中，AB=AC，D、E分别为AC、AB的中点．